Часто приходится изображать на координатной плоскости мно­жество решений неравенства с двумя переменными. Решением неравенства с двумя переменными называют пару значений этих переменных, которая обращает данное неравенство в верное числовое неравенство.

Изобразим на координатной плоскости множество решений нера­венства 2у + Зх < 6.

Сначала построим прямую. Для этого запишем неравенство в виде уравнения 2у + Зх = 6 и выразим y. Таким образом, получим: y=(6-3x)/2.

Эта прямая раз­бивает множество всех точек координатной плоскости на точки, расположенные выше ее, и точки, расположенные ниже ее.

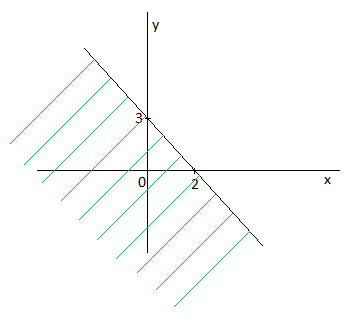
Возь­мем из каждой области по контрольной точке, например А (1;1) и В (1; 3)

Координаты точки А удовлетворяют данному неравенству 2у + Зх < 6, т. е. 2 • 1 + 3 • 1 < 6.

Координаты точки В не удовлетворяют данному неравенству 2∙3 + 3∙1 < 6.

Так как данное неравенство может изменить знак на прямой 2у + Зх = 6, то неравенству удовлетворяет множество точек той об­ласти, где расположена точка А. Заштрихуем эту область.

Таким образом, мы изобразили множество решений неравенства 2у + Зх < 6.

Пример

Изобразим множество решений неравенства х² + 2х + у² - 4у + 1 > 0 на координатной плоскости.

Построим сначала график уравнения х² + 2х + у² - 4у + 1 = 0. Вы­делим в этом уравнении уравнение окружности: (х² + 2х + 1) + (у² - 4у + 4) = 4, или (х + 1)² + (у - 2)² = 2².

Это уравнение окружности с центром в точке 0 (-1; 2) и радиусом R = 2. Построим эту окружность.

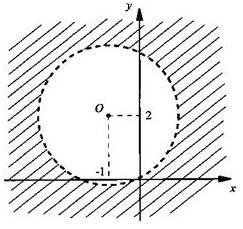
Так как данное неравенство строгое и точки, лежащие на самой окружности, неравенству не удовлетворяют, то строим окружность пунктирной линией.

Легко проверить, что координаты центра О окружности данному неравенству не удовлетворяют. Выражение х² + 2х + у² - 4у + 1 ме­няет свой знак на построенной окружности. Тогда неравенству удовлетворяют точки, расположенные вне окружности. Эти точки заштрихованы.

Пример

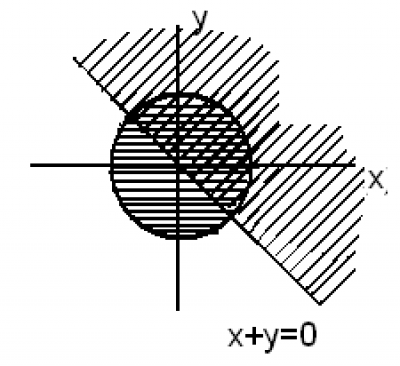
Изобразим на координатной плоскости множество решений нера­венства

(у - х²)(у - х - 3) < 0.

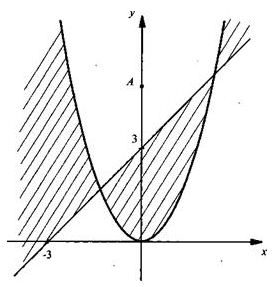
Сначала построим график уравнения (у - х²)(у - х - 3) = 0. Им яв­ляется парабола у = х² и прямая у = х + 3. Построим эти линии и отметим, что изменение знака выражения (у - х²)(у - х - 3) проис­ходит только на этих линиях. Для точки А (0; 5) определим знак это­го выражения: (5- 3) > 0 (т. е. данное неравенство не выполняется). Теперь легко отметить множество точек, для кото­рых данное неравенство выполнено (эти области заштрихованы).

Алгоритм решения неравенств с двумя переменными

1. Приведем неравенство к виду f (х; у) < 0 (f (х; у) > 0; f (х; у) ≤ 0; f (х; у) ≥ 0;)

2. Записываем равенство f (х; у) = 0

3. Распознаем графики, записанные в левой части.

4. Строим эти графики. Если неравенство строгое (f (х; у) < 0 или f (х; у) > 0), то - штрихами, если неравенство нестрогое (f (х; у) ≤ 0 или f (х; у) ≥ 0), то - сплошной линией.

5. Определяем, на сколько частей графики разбили координатную плоскость

6. Выбираем в одной из этих частей контрольную точку. Определяем знак выражения f (х; у)

7. Расставляем знаки в других частях плоскости с учетом чередования (как по методу интервалов)

8. Выбираем нужные нам части в соответствии со знаком неравенства, которое мы решаем, и наносим штриховку