В данной статье предложены примеры и решения содержательных задач с использованием математического аппарата.

В первую очередь рассмотрим несколько советов, которые помогают понять, с чего начинать решение любой задачи и как действовать поэтапно.

Сначала прочитайте задачу ознакомительно. Нужно попытаться получить информацию и представить ее в другом виде: рисунок, таблица или просто краткая запись условия задачи. При решении задач короткую запись задачи можно сделать с помощью рисунка или таблицы. Таблица является универсальным средством и позволяет решать большое количество идейно близких задач.

Второе прочтение имеет своей целью выбор неизвестных, при этом не обращаем внимание на числа и «мелочи». Главное, чтобы неизвестные соответствовали условию задачи, при составлении соответствующей “математической модели” (уравнение, неравенство, система уравнений или неравенств). При третьем прочтении задачи следует ее условие расчленить на логические части. Необходимо следить за тем, что соответствует каждой фразе текста задачи в полученной математической записи и чему в тексте задачи соответствует каждый “знак” полученной записи (сами неизвестные, действия над ними, полученные уравнения, неравенства или их системы).

Очень важно не только составить уравнение, неравенство, систему уравнений или неравенств, но и решить составленное. Если решение задачи не получается, то нужно ещё раз прочитать и проанализировать задачу (заданный текст и полученную запись). Иногда по условию задачи достаточно отыскать не сами неизвестные, а их комбинации.

Можно выделить вопросы, которые дают верное направление решению задач разных типов:

О каком процессе идёт речь? Какими величинами характеризуется этот процесс? (Количество величин соответствует числу столбцов таблицы).

Сколько процессов в задаче? (Количество процессов соответствует числу строк в таблице).

Какие величины известны? Что надо найти? (Таблица заполняется данными задачи; ставится знак вопроса).

Как связаны величины в задаче? (Вписать основные формулы, выяснить связи и соотношения величин в таблице).

Какую величину (величины) удобно выбрать в качестве неизвестной или неизвестных? (Клетки в таблице заполняются в соответствии с выбранными неизвестными).

Какие условия используются для составления “модели”? (Выписать полученную “модель”)

Легко ли решить полученное? (Если решить сложно, ввести новые переменные, использовать другие соотношения).

Рассмотрим примеры

Пример 1

Решено комнату ( включая потолок) оклеить обоями. Обои покупаются с запасом 20% от оклеиваемой площади. Стоимость обоев указана в таблице. Потолок решено оклеить белыми обоями, стены - зелеными.

Ширина двери комнаты равна 0,8 м, высота - 2 м. Ширина окна - 1,5 м, высота - 1 м. Сколько рублей надо заплатить за обои, если эскиз комнаты представлен на рисунке?

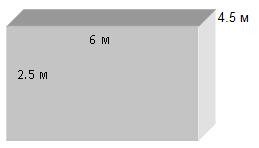
Решение:

1. Посчитаем площадь стен комнаты:

\(S = 2,5 \cdot 2 \cdot (6 + 4,5) = 52,2\)

1. Вычтем площади окна и двери:

\({S_1} = 52,2 - 0,8 \cdot 2 - 1,5 \cdot 1 = 49,4\)

1. Тогда зеленых обоев с запасом 20% необходимо купить по цене 11 руб.:

\(Su{m_1} = 49,4 \cdot 11 \cdot 1,2 = 652,08\)

1. Посчитаем площадь потолка:

\({S_3} = 4,5 \cdot 6 = 27\)

1. Тогда белых обоев с запасом 20% необходимо купить по цене 14 руб.:

\(Su{m_2} = 27 \cdot 14 \cdot 1,2 = 453,6\)

1. Итого заплатить необходимо 1105,68 рублей.

Пример 2

Интернет-провайдер (компания, оказывающая услуги по подключению к сети Интернет) предлагает три тарифных плана.

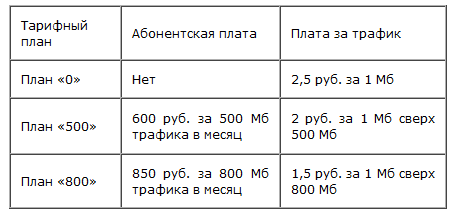
Пользователь планирует, что его трафик составит 600 Мб и, исхо­дя из этого, выбирает наиболее дешевый тарифный план. Сколько рублей должен заплатить пользователь за месяц, если его трафик дей­ствительно будет равен 600 Мб?

Решение:

Просчитаем затраты по каждому варианту тарифных планов:

1. \({S_1} = 2,5 \cdot 600 = 1500\)
2. \({S_2} = 600 + 2 \cdot 100 = 800\)
3. \({S_3} = 850\)

Таким образом, самым выгодным оказывается второй тарифный план «500»