Конденсатор состоит из двух, первоначально незаряженных, пластин. Будем постепенно отнимать у нижней пластины заряд dq и переносить его на верхнюю пластину (рис. 1.6.7).

В результате между пластинами возникнет разность потенциалов \({\phi _2} - {\phi _1}.\) При переносе каждой порции заряда совершается элементарная работа

\(\delta A = - {\rm{d}}q({\phi _2} - {\phi _1}).\)

Воспользовавшись определением емкости \(C = \frac{q}{{{\phi _1} - {\phi _2}}},\) получаем

\(\delta A = \frac{{q{\rm{d}}q}}{C}\).

Общая работа, затраченная на увеличение заряда пластин конденсатора от 0 до q, равна

 \(A = \int\limits_0^q {\delta A} = \int\limits_0^q {\frac{{q{\rm{d}}q}}{C}} = \frac{{{q^2}}}{{2C}}.\) (1.6.16)

При вычислении интеграла учтено, что емкость С не зависит от q и φ. Величина полной работы А равна энергии, запасенной конденсатором,

\(W = \frac{{{q^2}}}{{2C}} = \frac{{q\left( {{\varphi _1} - {\varphi _2}} \right)}}{2} = \frac{{qU}}{2}\). (1.6.17)

Эту энергию можно также записать в виде

\(W = \frac{1}{2}C{\left( {{\phi _1} - {\phi _2}} \right)^2} = \frac{1}{2}C{U^2}.\) (1.6.18)

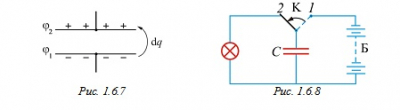
Запасание энергии конденсатором наглядно проявляется при его подключении к электрической лампочке. Лампочка вспыхивает и гаснет при разрядке конденсатора (рис. 1.6.8).

Вспомним понятиепондермоторные силы – силы электрического взаимодействия между пластинами конденсатора. Эту силу можно вычислить через энергию взаимодействия.

При незначительном перемещении одной пластины в поле другой совершается работа

\({\rm{\delta }}A = - {\rm{d}}W = F{\rm{d}}x\),

отсюда \(F = - \frac{{{\rm{d}}W}}{{{\rm{d}}x}}.\) 

Продифференцируем выражение для энергии конденсатора (1.6.17) и, подставив значение емкости конденсатора С, получим

\(F = - \frac{{{\rm{d}}W}}{{{\rm{d}}x}} = - \frac{{{q^2}}}{{2{\varepsilon _0}\varepsilon S}}\).

Модуль этого выражения дает величину пондермоторной силы

 \(F = \frac{{{q^2}}}{{2{\varepsilon _0}\varepsilon S}}.\) (1.6.19)