Имеется много случаев, когда масса тела изменяется в процессе движения за счет непрерывного отделения или присоединения вещества (ракета, реактивный самолет, автомобиль для поливки улицы).

Наша задача: найти уравнение движения такого тела. Решение этого вопроса покажем на примере ракеты. Принцип действия ракеты состоит в следующем. Ракета с большой скоростью выбрасывает вещество (продукты сгорания), воздействуя на него с большой силой. Выбрасываемое вещество с такой же, но противоположно направленной силой, в свою очередь, действует на ракету и сообщает ей ускорение в противоположном направлении.

Пусть в момент времени t масса ракеты m, а ее скорость \(\vec v\). Спустя время dt ее масса уменьшилась на dm и стала равной m – dm, а скорость стала равной \(\vec v + {\rm{d}}\vec v\). Изменение импульса системы за время dt равно

\({\rm{d}}\vec P = \left[ {\left( {m - {\rm{d}}m} \right)\left( {\vec v + {\rm{d}}\vec v} \right) + {\rm{d}}m\left( {\vec v + {\rm{d}}\vec v + \vec u} \right)} \right] - m\vec v\), (6.9)

где \(\vec u\) – скорость истечения газов относительно ракеты. Раскроем скобки в этом уравнении, получим

\({\rm{d}}\vec P = m{\rm{d}}\vec v + \vec u{\rm{d}}m\). (6.10)

Так как на ракету действуют внешние силы 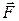 (сила тяжести, сила сопротивления воздуха), то согласно (3.3)

\(\vec F{\rm{d}}t = m{\rm{d}}\vec v + \vec u{\rm{d}}m\) или \(m\frac{{{\rm{d}}\vec v}}{{{\rm{d}}t}} = \vec F - \vec u\frac{{{\rm{d}}m}}{{{\rm{d}}t}}\). (6.11)

Величина \( - \vec u\frac{{{\rm{d}}m}}{{{\rm{d}}t}} = {\vec F_{р\rm{}}}\) называется реактивной силой. Это сила, с которой действуют на ракету вылетающие газы.

Тогда

\(m\vec a = \vec F + {\vec F_{р\rm{}}}\) (6.12)

– уравнение движения тела с переменной массой (уравнение Мещерского).

Полученной формулой можно воспользоваться для расчета зависимости скорости ракеты от массы сгоревшего топлива. Будем считать, что внешние силы равны нулю, т.е. движение происходит только под действием реактивной силы:

\(m\frac{{{\rm{d}}\vec v}}{{{\rm{d}}t}} = - \vec u\frac{{{\rm{d}}m}}{{{\rm{d}}t}}\). (6.13)

Если ракета движется прямолинейно, то \(v = - u\int {\frac{{{\rm{d}}m}}{m} = - u\ln m + C} \).

Значение постоянной интегрирования С определим из начальных условий. Пусть в начальный момент времени скорость ракеты равна нулю, а масса равна \({m_0}\). Отсюда С = u lnm₀. Следовательно,

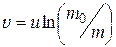. (6.14)

Это выражение называется формулой Циолковского. Она показывает, что при данной скорости истечения газов скорость ракеты определяется только отношением начальной массы \({m_0}\) ракеты к оставшейся массе m.