Пусть а – любое действительное число; n - натуральное число, \(n > 1.\)

Тогда n -ной степенью числа a называется произведение n множителей, каждый из которых равен a .

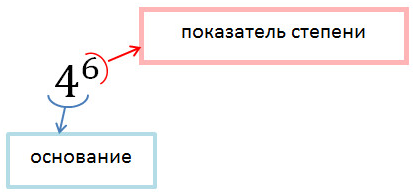
Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение. Так, вместо произведения шести одинаковых множителей 4 · 4 · 4 · 4 · 4 · 4 пишут 4⁶ и произносят «четыре в шестой степени».

4 · 4 · 4 · 4 · 4 · 4 = 4⁶

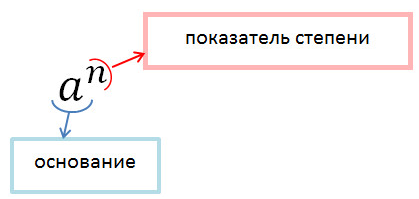
Число a называется основанием степени , число n - показателем степени .

• Если n = 1, то по определению считают:

\({a^1} = a.\)

• Любое число в нулевой степени равно единице:

\({a^0} = 1.\)

• Ноль в любой натуральной степени равен нулю:

\({0^n} = 0.\)

• Единица в любой степени равна 1:

\({1^n} = 1.\)

При решении примеров нужно помнить, что возведением в степень называется нахождение значения степени.

Возведение в степень отрицательного числа

Основание степени (число, которое возводят в степень) может быть любым числом -положительным, отрицательным или нулём.

• При возведении в степень положительного числа получается положительное число.
• При возведении нуля в натуральную степень получается ноль.

Свойства степеней с целым показателем:

\(\begin{gathered} {a^n} \cdot {a^k} = {a^{n + k}}; \\ {a^n}:{a^k} = {a^{n - k}}; \\ {({a^n})^k} = {a^{nk}}; \\ {a^n} \cdot {b^n} = {\left( {ab} \right)^n}; \\ \frac{{{a^n}}}{{{b^n}}} = {\left( {\frac{a}{b}} \right)^n}; \\ {a^{ - n}} = \frac{1}{{{a^n}}}; \\ {\left( {\frac{a}{b}} \right)^{ - n}} = {\left( {\frac{b}{a}} \right)^n}. \\ \end{gathered} \)

Примеры

Вычислите:

\(\begin{gathered} \frac{3}{{{5^{ - 2}}}} = 3 \cdot {5^2} = 3 \cdot 25 = 75; \\ {(0,1)^{ - 4}} = {\left( {\frac{1}{{10}}} \right)^{ - 4}} = {10^4} = 10000; \\ \frac{{{3^5} \cdot {3^{10}}}}{{{3^6} \cdot {3^7}}} = {3^{15}} \cdot {3^{ - 13}} = {3^2} = 9. \\ \end{gathered} \)

Упростите:

\(\begin{gathered} {\left( {{a^2}} \right)^{ - 3}} \cdot {a^9} = {a^{2 \cdot ( - 3)}} \cdot {a^9} = {a^{ - 6 + 9}} = {a^3}; \\ \frac{{{{\left( {{t^4}} \right)}^{ - 2}}}}{{{t^{ - 3}}}} = \frac{{{t^{ - 8}}}}{{{t^{ - 3}}}} = {t^{ - 8 - ( - 3)}} = {t^{ - 5}}. \\ \end{gathered} \)