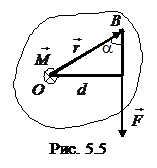
Рассмотрим вращение тела вокруг неподвижной оси (рис. 5.5). Пусть сила \(\vec F\) лежит в плоскости, перпендикулярной к оси вращения 0; \(\vec r\) – радиус-вектор точки приложения силы относительно оси вращения; d – кратчайшее расстояние от оси вращения до линии действия силы, называемое плечом силы.

Векторная величина, численно равная произведению силы на плечо, называется моментом силы относительно оси вращения:

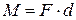. (5.14)

Как видно из рисунка:

 \(d = r \cdot \sin \alpha \);
 \(M = F \cdot r \cdot \sin \alpha \),

т.е. в векторном виде

\(\vec M = \left[ {\vec r\vec F} \right]\). (5.15)

Направление \(\vec M\) совпадает с направлением поступательного движения винта при его вращении от \(\vec r\) к \(\vec F\) (в нашем примере вдоль оси вращения «от нас»).

В частном случае, когда \(\alpha = 0,{\rm{ }}M = 0\) (линия действия силы пересекает ось вращения). Такая сила уравновешивается реакцией опоры и вращения не вызывает.