Когда сведений очень много, их нужно упорядочивать. Таблица – самый простой способ упорядочить данные. С некоторыми таблицами вы уже имели дело. Это таблицы сложения и умножения чисел, таблицы спряжения глаголов. Таблицами являются: расписание уроков, страницы школьного дневника, оглавление учебника. Таблицы облегчают поиск необходимых сведений, не заставляя изучать всю имеющуюся информацию.Однако таблицы не дают наглядного представления о соотношении величин. Для этого служат различные диаграммы: столбиковые, круговые, рассеивания и др. Пословица гласит: «Лучше один раз увидеть».

Диаграммы используются для наглядного, запоминающегося изображения и сопоставления данных.Таблицы и диаграммы удобно применять для сравнения шансов случайных событий, используя статистические данные (числовые данные, полученные в результате различных наблюдений, опросов, экспериментов.)На основе собранных статистических данных вычисляют частоту случайного события и выясняют, как она связана с вероятностью.Чтобы выяснить, насколько вероятно то или иное случайное событие, связанное со случайным экспериментом (эксперимент, условиями которого являются непредсказуемость и возможность многократного повторения), нужно подсчитать, как часто оно происходит. Для этого используют две важные величины – абсолютную и относительную частоту.

Абсолютная частота показывает, сколько раз в серии экспериментов наблюдалось данное событие. Это всегда целое число.

Относительная частота (частота n / N ) показывает, какая доля экспериментов завершилась наступлением данного события. Она равна отношению n — числа опытов, в которых интересующее нас событие произошло, к N — общему числу проведенных опытов. Это дробное число, меняющееся от 0 до 1. Опытным путем установлено, что проводя эксперименты огромное количество раз (больше 1000), например, такие эксперименты, как бросание игральной кости, бросание монеты, раздача игральных карт, розыгрыш лотереи и др., частоты становятся устойчивыми. Например, изобразим график зависимости частоты от числа опытов при бросании игральной кости, показывающий как часто выпадала "единица"

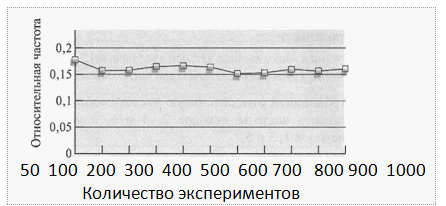
Другой пример. Событие А — «на кубике выпало четное число очков», событие В — «на кубике выпало нечетное число очков».

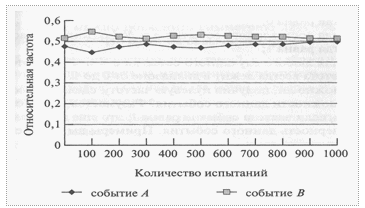
Устойчивость частот является скорее математическим, а не экспериментальным фактом. На нем основывается частотное, илистатистическое определение вероятности: за вероятность случайного события можно приближенно принять его относительную частоту.В теории вероятностей величина, значение которой зависит от исхода эксперимента, называется случайной величиной. Мы будем рассматривать ряд числовых значений такой величины, полученных в какой-либо серии экспериментов. Такой числовой ряд называется случайной выборкой.

Представим себе, что из всех школьников вашего региона случайным образом выбирается 1000 человек и фиксируется их оценка по математике в последней четверти. В статистике множество всех школьников региона будет называться генеральной совокупностью, а случайно выбранная 1000 школьников — случайной выборкой. Однако математики предпочитают иметь дело не со школьниками, а с числами, поэтому мы с вами будем называть случайной выборкой только числовой ряд — т. е. в нашем случае не самих выбранных школьников, а их оценки.