Функция - это одно из основных общенаучных и математических понятий, выражающее зависимость между переменными величинами. Это закон, по которому каждому значению элемента x из некоторого множества X ставится в соответствие единственный элемент y из множества Y.

Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом, а переменную у - зависимой переменной. Значение у, соответствующее заданному значению х, называют значением функции.

Записывают: у = f (х). Буквой f обозначается данная функция, т. е. функциональная зависимость между переменными х и у; f (х) есть значение функции, соответствующее значению аргумента х. Говорят также, что f (х) есть значение функции в точке х. Все значения, которые принимает независимая переменная, образуют область определения функции. Все значения, которые принимает функция f (х) (при х, принадлежащих области ее определения), образуют область значений функции.

Способы задания функции

Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у = f (х),

где f (х) - некоторое выражение с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.

Пусть функция задана аналитически формулой у = f (х). Если на координатной плоскости отметить все точки, обладающие следующим свойством: абсцисса точки принадлежит области определения функции, а ордината равна соответствующему значению функции, то множество точек (х; f (x)) есть график функции. В физике и технике функции нередко задаются графически, причем иногда гарфик является единственным доступным средством задания функции. Чаще всего это бывает при употреблении самопишущих приборов, автоматически записывающих изменение одной величины в зависимости от изменения другой. В результате на ленте прибора получается линия, графически задающая регистрируемую прибором функцию.

Также функцию можно задать таблично. Рассмотрим примеры функциональной зависимости в реальной жизни.

Пример 1

Таблицей заданы данный о росте ребенка в течении первых 5 месяцев жизни:

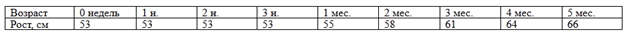
Имея таблицу значений функциональной зависимости роста от возраста, можно по точкам построить график:

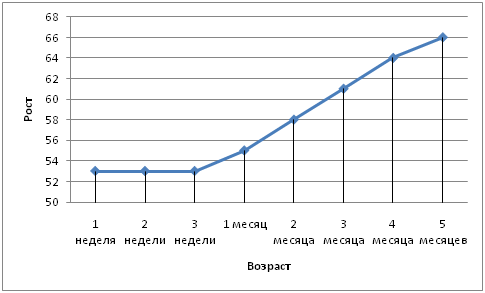
Пример 2

Вот яркий пример функции, заданной графически. На графике можно увидеть максимум и минимум, фрагменты линейной функции, сглаживание линий и т.д.

Кардиограмма - график работы сердца.

Кардиограмма - это запись сокращений сердца человека, которая осуществляется при помощи какого-либо инструментального способа. Во время сокращения сердце передвигается в пределах грудной клетки, оно вращается вокруг своей оси слева направо.

Суть электрографии заключается в том, чтобы зарегистрировать разности потенциала во времени. Кривая, которая показывает нам эти изменения и есть кардиограмма. Прибор, который записывает эту кривую, именуется электрокардиографом. Кардиограмма сердца показывает возбуждение сердца и его сокращение. Во время снятия кардиограммы к телу человека прикрепляются специальные электроды, благодаря которым аппарат и получает необходимые данные.

Суть обработки сигналов данного исследования заключается в том, чтобы диагностировать имеющиеся проблемы в работе сердечных мышц, используя при этом различные аналитические методы.

Пример 3

Переход вещества из твердого состояние в жидкое называется плавлением. Для того чтобы тело начало плавиться, его необходимо нагреть до определенной температуры. Температура, при которой вещество плавится, называют температурой плавления вещества.

Каждое вещество имеет свою температуру плавления. У каких-то тел она очень низкая, например, у льда. А у каких-то тел температура плавления очень высокая, например, железо. Плавление кристаллического тела это сложный процесс.

На рисунке представлен известный из курса физики график плавления льда.

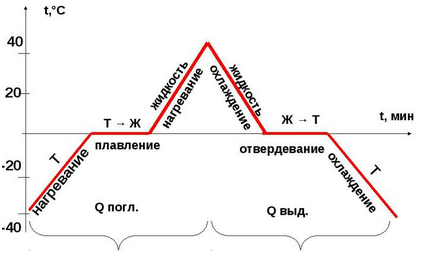
График показывает зависимость температуры льда от времени, которое его нагревают. На вертикальной оси отложена температура, по горизонтальной - время.

Из графика видно, что изначально температура льда была -40 градусов. Потом его начали нагревать. С течением времени, температура увеличилась до 0 градусов. Эта температура считается температурой плавления льда. При этой температуре лед начал плавиться, но при этом перестала возрастать его температура, хотя при этом лед также продолжали нагревать. Затем, когда весь лед расплавился и превратился в жидкость, температура воды снова стала увеличиваться. Во время плавления температура тела не изменяется, так как вся поступающая энергия идет на плавление. После нагревания (пик графика) жидкость стали охлаждать, процесс пошел в обратную сторону до затвердевания.

Рассмотрим задачу

Туристы отправились с турбазы на озеро, провели там 2 часа и вернулись обратно. Выберите график, описывающий зависимость пройденного расстояния от времени:

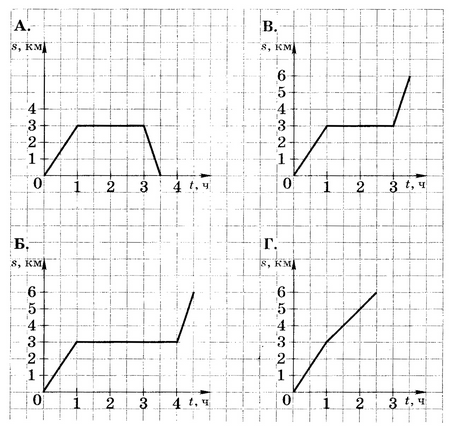
Верным будет ответ А., т.к. в течении двух часов туристы находились на озере, добравшись до него, а затем снова вернулись в лагерь, т.е. в нулевую точку отсчета.