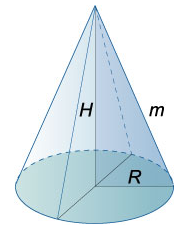
Радиус основания кругового конуса: R

Образующая конуса: m

Высота конуса: H

Объем конуса: V

Площадь основания: S_осн

Площадь боковой поверхности: S_бок

Площадь полной поверхности: S

1. Конус или коническая поверхность представляет собой пространственную фигуру, образованную движением прямой, проходящей через некоторую определенную точку (вершину конуса) и пересекающую заданную линию, которая называется направляющей конуса. Указанная прямая называется образующей. Часто конусом называется пространственная фигура, ограниченная внутренней частью плоскости, пересекающей коническую поверхность, и частью конической поверхности, заключенной между вершиной и границей пересечения. Часть указанной плоскости, лежащая внутри конической поверхности, называется основанием конуса, а часть конической поверхности − боковой поверхностью.

2. Конус называется круговым, если в его основании лежит круг.

3. Конус является прямым, если его вершина проецируется в центр основания.

4. Прямой круговой конус образуется при вращении прямоугольного треугольника вокруг его катета. Прямой круговой конус определяется радиусом основания R и высотой H (или радиусом основания R и образующей m).

1. Соотношение между высотой, радиусом основания и образующей в прямом круговом конусе 
   \(H = \sqrt {{m^2} - {R^2}} \)

2. Площадь боковой поверхности прямого кругового конуса 
   S_бок=_πRm

3. Площадь основания кругового конуса 
   S_осн=_πR²

4. Площадь полной поверхности прямого кругового конуса 
   S=S_бок+S_осн=_πR(m+R)

5. Объем кругового конуса 
   \(V = \frac{{{S_{OCH}}H}}{3} = \frac{{\pi {R^2}H}}{3}\)