Математика
3.2.2. Четность и нечетность функции
Четность и нечетность функции
Четность и нечетность функции
К важнейшим свойствам функций относится четность/нечетность.
Функция называется нечетной, если при изменении знака аргумента, она меняет свое значение на противоположное. Формульная запись этого выглядит так \(f( - x) = - f(x).\) Это значит, что после подстановки в функцию на место всех иксов значений «минус икс», функция изменит свой знак. График такой функции симметричен относительно начала координат.
Примерами нечетных функций являются:
\(\begin{gathered} y = x; \\ y = {x^3}; \\ y = \sin x; \\ \end{gathered} \)
и другие.
Посмотрим на графическое изображение таких функций и симметричность относительно точки (0;0).
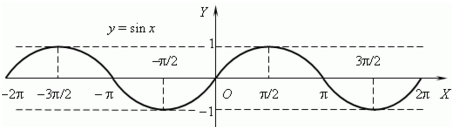
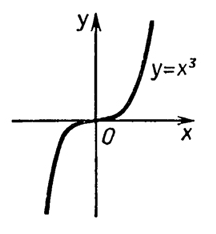
Функция называется четной, если при изменении знака аргумента, она не меняет свое значение. Формульная запись этого выглядит так \(f( - x) = f(x).\). Это значит, что после подстановки в функцию на место всех иксов значений «минус икс», функция в результате не изменится. График такой функции симметричен относительно оси Оу.
Примерами четных функций являются:
\(\begin{gathered} y = |x|; \\ y = {x^2}; \\ y = \cos x; \\ \end{gathered} \)
и другие.
Покажем симметричность функции модуля y=|x|. Аналитически по правилу \(y( - x) = | - x| = |x| = y,\) т.е. функция четная.
Графически:
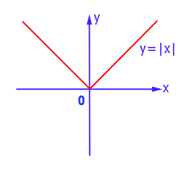
Важно! Если функция не относится ни к одному из указанных видов, то ее не называют ни четной, ни нечетной. Она является функцией общего вида. И у таких функций нет симметрии.
Рассмотрим функцию \(y(x) = 5 - 3x.\) Проверим ее на четность/нечетность:
\(y( - x) = 5 - 3 \cdot ( - x) = 5 + 3x \ne \left\{ \begin{gathered} - y(x), \\ y(x). \\ \end{gathered} \right.\)
Таким образом, это функция общего вида, которая не имеет симметрии. Посмотрим на ее вид на графике:
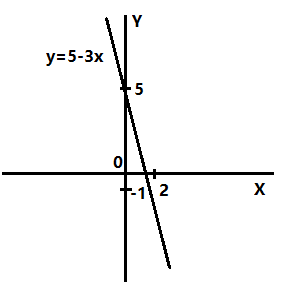
Другие материалы по данной теме
Формула
f(-x)=f(x)