Рассмотрим на координатной плоскости XOY окружность единичного радиуса с центром в начале координат. Неподвижный луч OA с центром в O(0, 0) и подвижный луч OB образуют угол α.

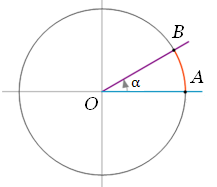
Если вращение от неподвижного луча подвижного луча происходит против часовой стрелки, то угол считается положительным, а если вращение происходит по часовой стрелки, то угол считается отрицательным.
Единицы измерения: градус, радиан.
Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в 1 радиан.

\(1рад. = \frac{{{{180}^0}}}{\pi }\)

Так как π ≈ 3.14, то 1 рад. ≈ 57.3°.

Если угол содержит α радиан, то его градусная мера:

\(\begin{array}{l}\alpha рад. = {\left[ {\frac{{180}}{\pi }} \right]^0};\\{1^0} = \frac{\pi }{{{{180}^0}}}рад.,\mathop {}\nolimits_{}^{} {\alpha ^0} = \frac{\pi }{{{{180}^0}}} \cdot \alpha рад.\end{array}\)

Переход от радианной меры угла к градусной:

\(\begin{array}{l}\pi рад. - {180^0};\\\alpha рад. - {n^0};\\ \Rightarrow {n^0} = \frac{{{{180}^0}}}{\pi } \cdot \alpha .\end{array}\)

Переход от градусной меры к радианной мере угла:

\(\alpha рад. = \frac{{\pi n}}{{{{180}^0}}} \cdot \)

Следует избегать равенства вида \({90^0} = \frac{\pi }{2}\) потому, что они не являются числовыми равенствами, а лишь означают, что 90° и π/2 радиан являются различными мерами измерения одного и того же угла.

Углы можно отметить на тригонометрическом круге.

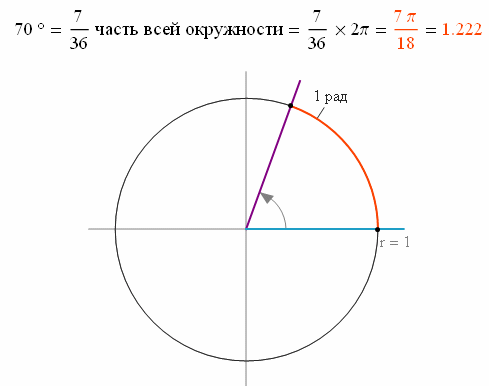
Заметим, что каждой точке единичной окружности соответствует не одно, а бесконечно много действительных чисел.