Сила трения скольжения\({\vec F_{{\rm{тр}}{\rm{.ск}}}}\), возникает при перемещении (скольжении) соприкасающихся тел друг относительно друга. Приложенная к бруску сила трения скольжения направлена вдоль поверхности соприкосновения тел и противоположна скорости бруска. Явление сухого трения изучено Кулоном и Амонтоном. Из опыта известно, что модуль силы трения скольжения пропорционален силе нормального давления или, что то же самое, силе нормальной реакции опоры N (\(N = {F_n}\)). Сила трения скольжения равна

\({F_{{\rm{тр}}{\rm{.ск}}}} = \mu {F_n} = \mu \cdot N\), (3.9)

где m – коэффициент трения скольжения, зависящий от природы и состояния соприкасающихся поверхностей.

Сила трения скольжения возникает при относительном скольжении тела по поверхности контакта, поэтому сила трения скольжения является функцией относительной скорости. В векторной форме закон Кулона – Амонтона для силы сухого трения имеет вид

\({\vec F_{{\rm{тр}}{\rm{.ск}}}} = - \mu N\frac{{\vec v}}{v}\), (3.10)

где \(\frac{{\vec v}}{v} = {\vec \ell _v}\) – единичный вектор в направлении движения тела относительно поверхности, по которой движется тело. Скорость \(\vec v\) имеет смысл относительной скорости, т.е. скорости тела по отношению к поверхности, по которой движется тело. Коэффициент трения скольжения μ является функцией относительной скорости движения тел \(\mu = \mu (v{\rm{)}}\), однако эта зависимость является слабой и в большинстве случаев ею можно пренебречь, считая коэффициент трения скольжения постоянной величиной.

Если тело движется по горизонтальной поверхности, то сила нормального давления численно равна силе тяжести (\(N = mg\)), тогда \({F_{{\rm{тр}}{\rm{.ск}}}} = \mu \;mg\).

Если тело движется вдоль наклонной плоскости (рис. 3.6), то

\({F_{{\rm{тр}}{\rm{.ск}}}} = {\rm{\mu }} \cdot P \cdot \cos \alpha = {\rm{\mu }} \cdot mg \cdot \cos \alpha \). (3.11)

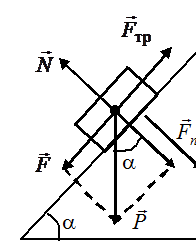Сила трения направлена в сторону, противоположную направлению движения данного тела относительно другого.

Вязкая среда (газ, жидкость) оказывает сопротивление движению тела. Из обобщения результатов эксперимента следует, что при малых скоростях тела \( {v_{{\rm{отн}}}}\) относительно вязкой среды сила сопротивления пропорциональна относительной скорости: \({F_{\rm{c}}} = \beta \cdot {v_{{\rm{отн}}}}\), где β – коэффициент сопротивления, зависящий от формы тела, вещества и температуры среды. Например, сила сопротивления, действующая на шарик радиуса R в жидкости, определяется законом \({F_{\rm{c}}} = 6\pi \eta R{v_{{\rm{отн}}}}\), где \(\beta = 6\pi \eta R\) и η – вязкость среды.

В векторной форме закон силы сопротивления имеет вид: \({\vec F_{\rm{c}}} = - \beta \cdot {\vec v_{{\rm{}}}}\).

При больших скоростях движения сила сопротивления начинает зависеть от скорости по закону \({F_{\rm{c}}} \~ v_{{\rm{}}}^{\rm{2}}\) или \({F_{\rm{c}}} \~ v_{{\rm{}}}^{\rm{3}}\). Такое наблюдается, например, при полете самолетов.