Очень важ­ным свой­ством функ­ции яв­ля­ет­ся ее мо­но­тон­ность. Зная это свой­ство раз­лич­ных спе­ци­аль­ных функ­ций, можно опре­де­лить по­ве­де­ние раз­лич­ных фи­зи­че­ских, эко­но­ми­че­ских, со­ци­аль­ных и мно­гих дру­гих про­цес­сов.

Монотонная функция -  это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называется строго монотонной. Т.е. монотонная функция - это функция, меняющаяся в одном и том же направлении.

Вы­де­ля­ют сле­ду­ю­щие виды мо­но­тон­но­сти функ­ций:

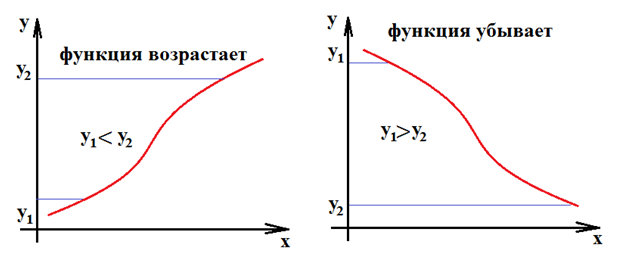
1. Функ­ция\(f(x)\)  воз­рас­та­ет, если на неко­то­ром ин­тер­ва­ле для любых двух точек x₁ и x₀ этого ин­тер­ва­ла таких, что \({x_2} > {x_1}\) вы­пол­не­но: \(f({x_2}) > f({x_1}).\)Т.е. боль­ше­му зна­че­нию ар­гу­мен­та со­от­вет­ству­ет боль­шее зна­че­ние функ­ции.
2. Функ­ция \(f(x)\) убывает, если на неко­то­ром ин­тер­ва­ле для любых двух точек x₁ и x₀ этого ин­тер­ва­ла таких, что \({x_2} > {x_1}\) вы­пол­не­но: \(f({x_2}) < f({x_1}).\)Т.е. боль­ше­му зна­че­нию ар­гу­мен­та со­от­вет­ству­ет меньшее зна­че­ние функ­ции.

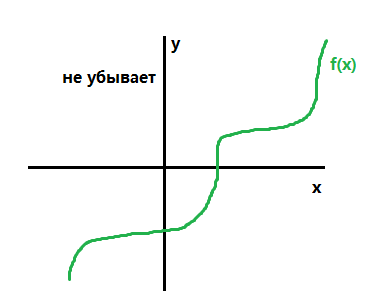
1. Функ­ция \(f(x)\) не убы­ва­ет, если на неко­то­ром ин­тер­ва­ле для любых двух точек x₁ и x₀ этого ин­тер­ва­ла таких, что \({x_2} > {x_1}\) вы­пол­не­но: \(f({x_2}) \geqslant f({x_1}).\)

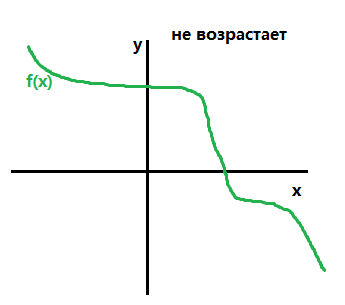
1. Функ­ция \(f(x)\) не возрастает, если на неко­то­ром ин­тер­ва­ле для любых двух точек x₁ и x₀ этого ин­тер­ва­ла таких, что \({x_2} > {x_1}\) вы­пол­не­но: \(f({x_2}) \leqslant f({x_1}).\)

Для пер­вых двух слу­ча­ев еще при­ме­ня­ют тер­мин «стро­гая мо­но­тон­ность».

Два по­след­них слу­чая яв­ля­ют­ся спе­ци­фи­че­ски­ми и за­да­ют­ся обыч­но в виде ком­по­зи­ции из несколь­ких функ­ций.

От­дель­но от­ме­тим, что рас­смат­ри­вать воз­рас­та­ние и убы­ва­ние гра­фи­ка функ­ции сле­ду­ет имен­но сле­ва напра­во и никак иначе.

Достаточные условия строгой монотонности функции, имеющей производную на интервале.

Если для любого значения х из (a;b) f'(x)>0, то f строго возрастает на (a;b).

Если для любого значения х из (a;b) f'(x)<0, то f строго убывает на (a;b).

Пример

Найти интервалы возрастания/убывания и экстремумы функции:

\(f(x) = - \frac{1}{3}{x^3} + 3{x^2} - 5x - 1.\)

Решение:

1) На первом шаге нужно найти область определения функции, а также взять на заметку точки разрыва (если они существуют). В данном случае функция непрерывна на всей числовой прямой, и данное действие в известной степени формально.

2) Второй пункт алгоритма обусловлен необходимым условием экстремума:

Если в точке x₀ есть экстремум, то либо f’(x₀)=0, либо значения f’(x₀) не существует.

\(\begin{gathered} f'(x) = - \frac{1}{3} \cdot 3{x^2} + 3 \cdot 2{x^{}} - 5 = 0; \ \Rightarrow {x_1} = 1;{x_2} = 5. \end{gathered} \)

Нашли критические точки.

- если при переходе через точку x₀ производная меняет знак с «плюса» на «минус», то в данной точке функция достигает максимума;

- если при переходе через точку x₀ производная меняет знак с «минуса» на «плюс», то в данной точке функция достигает минимума.

Таким образом, исходная функция достигает минимума в точке х=1, и ее значение там равно -3,33(3). Максимума функция достигает в точке х=5 со значением 7,33(3). Промежутки монотонности:

 \(\begin{gathered} ( - \infty ;1), (1;5), (5; + \infty ). \end{gathered} \)