Выражением вида a^(m/n), где n - некоторое натуральное число, m - некоторое целое число и основание степени а больше нуля, называется степень с дробным показателем. Причем верным является следующее равенство:

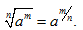
Числа вида m/n, где n – некоторое натуральное число, а m – некоторое целое число, называют дробными или рациональными числами. Из всего вышесказанного получаем, что степень определена для любого рационального показателя степени и любого положительного основания степени.

 Решение задач на преобразование выражений предполагает, как правило, последовательное упрощение данных выражений. При этом используются свойства степеней и формулы сокращенного умножения. В некоторых случаях (при упрощении выражений, содержащих корни или степени с дробным показателем) целесообразно сделать замену переменной. При этом в качестве новой переменной выбирается переменная (буква) в степени, знаменатель которой является наименьшим общим кратным знаменателей, а числитель – наибольшим общим делителем числителей в показателях степеней этой переменной. Такая замена позволяет перейти к выражениям, содержащим только целые степени переменных (букв).

Для любых рациональных чисел p,q и любых a>0 и b>0 верны следующие равенства:

1. (a^p)*(a^q) = a^(p+q)
2. (a^p):(b^q) = a^(p-q)
3. (a^p)^q = a^(p*q)
4. (a*b)^p = (a^p)*(b^p)
5. (a/b)^p = (a^p)/(b^p)

Данные свойства широко используются при преобразовании различных выражений, где содержатся степени с дробными показателями.

Примеры:

Пример 1.

Упростите выражение:

\(1 - {x^6}({x^{ - 2,7}} - {x^{ - 2,3}})({x^{ - 3,3}} + {x^{ - 2,9}} + {x^{ - 2,5}}).\)

Решение

Сделаем замену переменной. Пусть y=x^-0,1.

Выражение принимает вид:

\(\begin{gathered} 1 - {y^{ - 60}}({y^{27}} - {y^{23}})({y^{33}} + {y^{29}} + {y^{25}}) = \\ = 1 - {y^{ - 60}}{y^{23}}{y^{25}}({y^4} - 1)({y^8} + {y^4} + 1) = \\ = 1 - {y^{ - 12}}({y^{12}} - 1) = 1 - 1 + {y^{ - 12}} = {y^{ - 12}}. \\ \end{gathered} \)

Сделаем обратную замену. Получим x^6/5.

Упрощение выражений обычно сводится к приведению подобных членов и сокращению дробей после некоторых предварительных действий, важнейшим из которых является разложение на множители. Последнее, в свою очередь, заключается в выполнении одной или нескольких из следующих четырех «инструкций»:

1) группировка слагаемых;

2) вынесение за скобку;

3) применение формулы;

4) добавление и вычитание.

Пример2.

Упростите выражение:

\(13xy - 2ab - 7yx + 3ab.\)
Решение

Сгруппируем:

\(\begin{gathered} 13xy - 2ab - 7yx + 3ab = (13xy - 7yx) + (3ab - 2ab) = \\ = 6xy + ab. \\ \end{gathered} \)

Пример3.

Упростите выражение:

\(\frac{{3xy - 7xz}}{{3y - 7z}}.\)
Решение

Вынесем за скобку х в числителе:

\(\frac{{3xy - 7xz}}{{3y - 7z}} = \frac{{x(3y - 7z)}}{{3y - 7z}} = x.\)

Пример4.

Упростите выражение:

\(\frac{{9{y^4} - 4{x^2}}}{{2x + 3{y^2}}}.\)
Решение

В числителе применим формулу разности квадратов:

\(\frac{{9{y^4} - 4{x^2}}}{{2x + 3{y^2}}} = \frac{{(3{y^2} + 2x)(3{y^2} - 2x)}}{{2x + 3{y^2}}} = 3{y^2} - 2x.\)

Пример5.

Упростите выражение:

\(\frac{{4{a^4} + 1}}{{2{a^2} - 2a + 1}}.\)
 

Решение

В числителе добавим и вычтем слагаемое 4а²:

\(\begin{gathered} \frac{{4{a^4} + 1}}{{2{a^2} - 2a + 1}} = \frac{{4{a^4} + 4{a^2} + 1 - 4{a^2}}}{{2{a^2} - 2a + 1}} = \frac{{{{(2{a^2} + 1)}^2} - {{(2a)}^2}}}{{2{a^2} - 2a + 1}} = \\ = \frac{{(2{a^2} + 1 - 2a)(2{a^2} + 1 + 2a)}}{{2{a^2} - 2a + 1}} = 2{a^2} + 1 + 2a. \\ \end{gathered} \)