Математика
3.3.4. Степенная функция с натуральным показателем, ее график
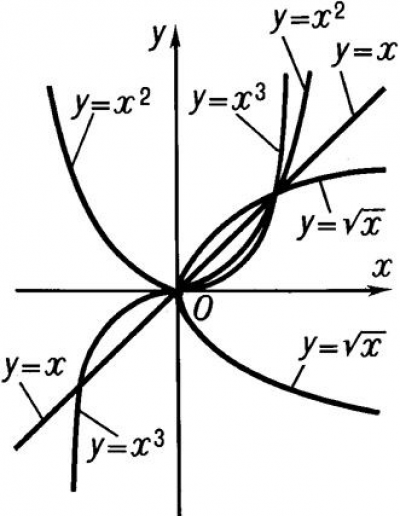
Степенная функция, ее свойства и графики
Рассмотрим степенную функцию \(y(x) = {x^p}\).
Показатель равен 0, р=0
Если показатель степенной функции \(y(x) = {x^p}\)равен нулю, p = 0, то степенная функция определена для всех x ≠ 0 и является постоянной, равной единице:
\(y(x) = {x^0} = 1,\) x ≠ 0 .
Показатель натуральный нечетный, р=1,3,5,…
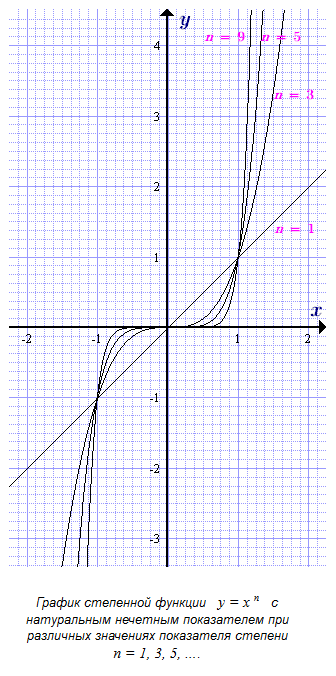
Рассмотрим степенную функцию \(y(x) = {x^p} = {x^n}\) с натуральным нечетным показателем степени n = 1, 3, 5, .... Такой показатель также можно записать в виде: n = 2k + 1, где k = 0, 1, 2, 3, ... - целое неотрицательное. Ниже представлены свойства и графики таких функций.
Область определения: –∞ < x < ∞
Множество значений: –∞ < y < ∞
Четность: нечетная, y(–x) = – y(x)
Монотонность: монотонно возрастает
Экстремумы: нет
Выпуклость:
при –∞ < x < 0 выпукла вверх
при 0 < x < ∞ выпукла вниз
Точки перегибов: x = 0, y = 0
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
\(\begin{gathered} \mathop {\lim }\limits_{x \to - \infty } {x^n} = \mathop {\lim }\limits_{x \to - \infty } {x^{2k + 1}} = - \infty ; \\ \mathop {\lim }\limits_{x \to + \infty } {x^n} = \mathop {\lim }\limits_{x \to + \infty } {x^{2k + 1}} = + \infty . \\ \end{gathered} \)
Частные значения:
при x = –1,
y(–1) = (–1) n ≡ (–1) 2k+1 = –1
при x = 0, y(0) = 0 n = 0
при x = 1, y(1) = 1 n = 1
Обратная функция:
при n = 1, функция является обратной к самой себе: x = y
при n ≠ 1, обратной функцией является корень степени n: \(x = \sqrt[n]{y}.\)
Показатель натуральный четный, р=2,4,6,…
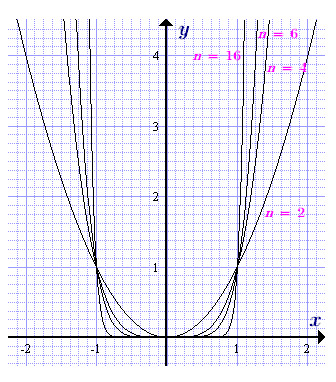
Рассмотрим степенную функцию \(y(x) = {x^p} = {x^n}\) с натуральным четным показателем степени n = 2,4,6, .... Такой показатель также можно записать в виде: n = 2k, где k = 0, 1, 2, 3, ... - натуральное. Ниже представлены свойства и графики таких функций.
Область определения: –∞ < x < ∞
Множество значений: 0 ≤ y < ∞
Четность: четная, y(–x) = y(x)
Монотонность:
при x < 0 монотонно убывает
при x > 0 монотонно возрастает
Экстремумы: минимум, x = 0, y = 0
Выпуклость: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
\(\begin{gathered} \mathop {\lim }\limits_{x \to - \infty } {x^n} = \mathop {\lim }\limits_{x \to - \infty } {x^{2k}} = + \infty ; \\ \mathop {\lim }\limits_{x \to + \infty } {x^n} = \mathop {\lim }\limits_{x \to + \infty } {x^{2k}} = + \infty . \\ \end{gathered} \)
Частные значения:
при x = –1, y(–1) = (–1) n ≡ (–1) 2k = 1
при x = 0, y(0) = 0 n = 0
при x = 1, y(1) = 1 n = 1
Обратная функция:
при n = 2, квадратный корень: \(x = \sqrt[{}]{y},y \geqslant 0;\)
при n ≠ 2, корень степени n: \(x = \sqrt[n]{y},y \geqslant 0.\)
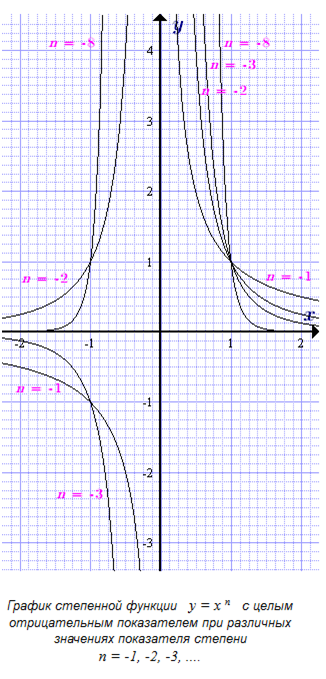
Степенная функция с целым отрицательным показателем, p = n = -1, -2, -3,...
Рассмотрим степенную функцию\(y(x) = {x^p} = {x^n}\) с целым отрицательным показателем степени n = -1, -2, -3, .... Если положить n = –k, где k = 1, 2, 3, ... – натуральное, то ее можно представить в виде:
\(y = {x^n} = {x^{ - k}} = \frac{1}{{{x^k}}}.\)
Нечетный показатель, n = -1, -3, -5,...
Ниже представлены свойства функции \(y(x) = {x^p} = {x^n}\)с нечетным отрицательным показателем n = -1, -3, -5,...
Область определения: x ≠ 0
Множество значений: y ≠ 0
Четность: нечетная, y(–x) = – y(x)
Монотонность: монотонно убывает
Экстремумы: нет
Выпуклость:
при x < 0: выпукла вверх
при x > 0: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: нет
Знак:
при x < 0, y < 0
при x > 0, y > 0
Пределы:
\(\begin{gathered} \mathop {\lim }\limits_{x \to - \infty } {x^n} = 0;\mathop {\lim }\limits_{x \to - \infty } {x^n} = - \infty ; \\ \mathop {\lim }\limits_{x \to + \infty } {x^n} = + \infty ;\mathop {\lim }\limits_{x \to + \infty } {x^n} = 0. \\ \end{gathered} \)
Частные значения:
при x = –1, y(–1) = (–1) n = –1
при x = 1, y(1) = 1 n = 1
Обратная функция:
при n = –1, \(x = \frac{1}{y};\)
при n < –2, \(x = \frac{1}{{\sqrt[{|n|}]{y}}}.\)
Четный показатель, n = -2, -4, -6,...
Ниже представлены свойства функции y = x n с четным отрицательным показателем n = -2, -4, -6, ....
Область определения: x ≠ 0
Множество значений: y > 0
Четность: четная, y(–x) = y(x)
Монотонность:
при x < 0: монотонно возрастает
при x > 0: монотонно убывает
Экстремумы: нет
Выпуклость: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: нет
Знак: y > 0
Пределы:
\(\begin{gathered} \mathop {\lim }\limits_{x \to - \infty } {x^n} = 0;\mathop {\lim }\limits_{x \to - \infty } {x^n} = - \infty ; l \\ \mathop {\lim }\limits_{x \to + \infty } {x^n} = + \infty ;\mathop {\lim }\limits_{x \to + \infty } {x^n} = 0. \\ \end{gathered} \)
Частные значения:
при x = –1, y(–1) = (–1) n = 1
при x = 1, y(1) = 1 n = 1
Обратная функция:
при n = –2, \(x = \frac{1}{{\sqrt[{}]{y}}};\)
при n < –2, \(x = \frac{1}{{\sqrt[{|n|}]{y}}}.\)
Другие материалы по данной теме
Видео
8.6. Степенная функция