Найдём работу, совершаемую при деформации упругой пружины.

Сила упругости \({F_{упр}} = - kx,\), где k – коэффициент упругости. Сила непостоянна, поэтому элементарная работа \({\rm{d}}A = F{\rm{d}}x = - kx{\rm{d}}x\) (знак минус говорит о том, что работа совершена над пружиной). Тогда

\(A = \int {{\rm{d}}A = - \int\limits_{{x_1}}^{{x_2}} {kx{\rm{d}}x = \frac{{kx_1^2}}{2} - \frac{{kx_2^2}}{2}} } ,\) (6.3.4)

т. е. А = Е_П1 - Е_П2 . Примем Е_п2 = 0, Е_п1 = Е_п, тогда

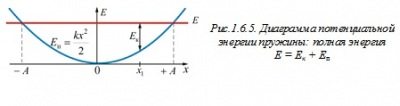
\({{\rm E}_\Pi } = \frac{{k{x^2}}}{2}\) . (6.3.5)

На рис. 1.6.5 показана диаграмма потенциальной энергии пружины. Здесь Е = Е_к + Е_п – полная механическая энергия системы, Е_к – кинетическая энергия в точке .