Математика
5.5.2. Угол между прямыми в пространстве, угол между прямой и плоскостью, угол между плоскостями
Вычисление углов в пространстве
Понятие о скалярном произведении позволяет достаточно просто определять углы между прямыми в пространстве. Действительно, пусть в пространстве заданы две прямые с направляющими векторами \(\vec a({a_1};{a_2};{a_3})\) и \(\vec b({b_1};{b_2};{b_3})\) Пусть угол между этими прямыми равен φ. Тогда угол между векторами может быть равен φ или180° – φ в зависимости от того, как направлены эти вектора. Однако в любом случае модуль скалярного произведения этих векторов равен
\(\left| {(\vec a,\vec b)} \right| = \left| {\vec a} \right|\left| {\vec b} \right|\cos \varphi \)
Отсюда следует, что \(\cos \varphi = \left| {\frac{{\vec a,\vec b}}{{\left| {\vec a} \right|\left| {\vec b} \right|}}} \right|,\) так как \(0 \leqslant \varphi \leqslant \frac{\pi }{2}.\) Итак, угол между двумя прямыми может быть найден через координаты направляющих векторов так
\(\cos \varphi = \left| {\frac{{\vec a,\vec b}}{{\left| {\vec a} \right|\left| {\vec b} \right|}}} \right|.\)
Покажем теперь, как можно вычислять угол между прямой и плоскостью. Поскольку угол между прямой и плоскостью есть угол между этой прямой и ее проекцией на эту плоскость, сведем данную задачу к предыдущей. Заметим, что угол между направляющим вектором рассматриваемой прямой и нормальным вектором равен
\(\frac{\pi }{2} - \varphi \).
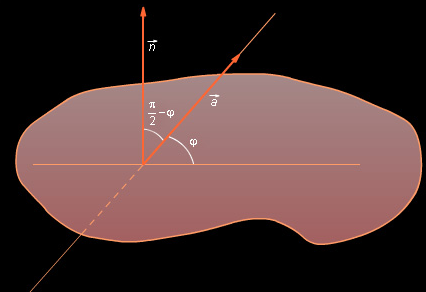
Рисунок 9.9.1
Этот угол уже легко вычисляется: \(\cos \left( {\frac{\pi }{2} - \varphi } \right) = \sin \varphi = \left| {\frac{{(\vec a,\vec b)}}{{\left| {\vec a} \right|\left| {\vec b} \right|}}} \right|.\) Значит угол между прямой и плоскостью равен
\(\sin \varphi = \left| {\frac{{(\vec a,\vec b)}}{{\left| {\vec a} \right|\left| {\vec b} \right|}}} \right|.\)
Найдем, наконец, угол между двумя плоскостями, если известны их нормальные векторы. Несложно сообразить, что угол между плоскостями равен углу между их нормалями. Докажите это утверждение самостоятельно.
| | |
Угол между плоскостями может быть найден по формуле:
\(\cos \varphi = \left| {\frac{{({{\vec n}_1},{{\vec n}_2})}}{{\left| {{{\vec n}_1}} \right|\left| {{{\vec n}_2}} \right|}}} \right|.\)
Другие материалы по данной теме
Видео
Видеоурок "Угол между плоскостями"
