В 1820 г. датский ученый Ганс Христиан Эрстед открыл явление отклонения магнитной стрелки гальваническим током и тем самым сделал первый существенный шаг в выяснении характера связи электрических и магнитных явлений. Затем французские ученые Гей-Люссак и Араго наблюдали намагничивание железа постоянным током, идущим в проводнике. Ампер обнаружил притяжение между проводами, по которым проходят параллельные токи, и отталкивание между противоположно направленными токами. Им же была выдвинута гипотеза о том, что свойства постоянных магнитов обусловлены циркулирующими в их толще постоянными круговыми токами (молекулярными токами).

Был сделан общий вывод: вокруг всякого проводника с током есть магнитное поле

Итак, вокруг всякого движущегося заряда помимо электрического поля существует еще и магнитное. Магнитное поле – это поле движущихся зарядов. Известно, что оно обнаруживает себя по действию на магнитные стрелки или на проводники с токами, т.е. на движущиеся заряды.

Дальше мы увидим, что, подобно электрическому полю, оно обладает энергией и, следовательно, массой. Магнитное поле материально. Теперь можно дать следующее определение магнитного поля: магнитное поле – это материя, связанная с движущимися зарядами и обнаруживающая себя по действию на магнитные стрелки и движущиеся заряды, помещенные в это поле.

Для анализа магнитного поля используются контуры с током.

Возьмем такой контур с током I и поместим его в магнитное поле.

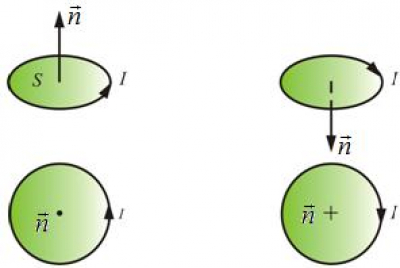
В магнитном поле контур с током будет ориентироваться определенным образом. Ориентацию контура в пространстве будем характеризовать направлением нормали \({\rm{\vec n}}\), связанной с движением тока правилом правого винта, или «правилом буравчика» (рис.).

Итак, на контур с током в магнитном поле действует вращающий момент. Контур ориентируется в данной точке поля только одним способом. Примем положительное направление нормали за направление магнитного поля в данной точке. Вращающий момент прямо пропорционален величине тока I, площади контура S и синусу угла между направлением магнитного поля и нормали :

\(M \sim IS{\rm{sin(}}\vec n{\rm{,}}\,\vec B{\rm{)}}{\rm{,}}\)

здесь М – вращающий момент, или момент силы; \(IS = {P_m}\) – магнитный момент контура (аналогично \(ql = \vec P\) – электрический момент диполя).

Направление вектора магнитногомомента совпадает с положительным направлением нормали:

\({\vec P_m} = {P_m}\vec n.\) (2.1.1)

Отношение момента силы к магнитному моменту\(\frac{M}{{{P_m}}}\) для данной точки магнитного поля будет одним и тем же и может служить характеристикой магнитного поля, названной магнитной индукцией:

\(B = \frac{M}{{{P_m}{\rm{sin}}(\vec n{\rm{,}}\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over B} )}}\,\,\), (2.1.2)

или \(\vec B = \frac{{{{\vec M}_{\max }}}}{{{{\vec P}_m}}},\) 

где \(\vec B\) – вектор магнитной индукции, совпадающий с нормалью \(\vec n\).

По аналогии с электрическим полем \(\vec E = \vec F{\rm{/}}q\).

Магнитная индукция \(\vec B\) характеризует силовое действие магнитного поля на ток (аналогично \(\vec E\) характеризует силовое действие электрического поля на заряд).