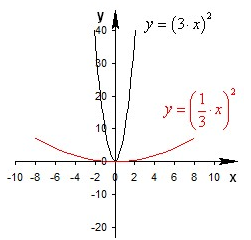В чистом виде основные элементарные функции встречаются, к сожалению, не так часто. Гораздо чаще приходится иметь дело с элементарными функциями, полученными из основных элементарных при помощи добавления констант и коэффициентов. Графики таких функций можно строить, применяя геометрические преобразования к графикам соответствующих основных элементарных функций (или переходить к новой системе координат).

С помощью геометрических преобразований графика функции f(x) может быть построен график любой функции вида \( \pm {k_1} \cdot f( \pm {k_2} \cdot (x + a)) + b,\) где \({k_1},{k_2} > 0\) - коэффициенты сжатия или растяжения (в зависимости от их значений) вдоль осей oy и ox соответственно. Знаки «минус» перед коэффициентами указывают на симметричное отображение графика относительно координатных осей, а и b определяют сдвиг относительно осей абсцисс и ординат соответственно.

Таким образом, различают три вида геометрических преобразований графика функции:

1. Первый вид - масштабирование (сжатие или растяжение) вдоль осей абсцисс и ординат.

На необходимость масштабирования указывают коэффициенты k₁ и k₂, отличные от единицы, если \(0 < {k_1} < 1,0 < {k_2} < 1\) , то происходит сжатие графика относительно oy и растяжение относительно ox , если \({k_1},{k_2} > 1\) , то производим растяжение вдоль оси ординат и сжатие вдоль оси абсцисс.

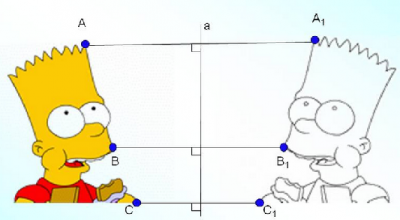
2. Второй вид - симметричное (зеркальное) отображение относительно координатных осей.

На необходимость этого преобразования указывают знаки «минус» перед коэффициентами k₁ (в этом случае симметрично отображаем график относительно оси ox ) и k₂ (в этом случае симметрично отображаем график относительно оси oy). Если знаков «минус» нет, то этот шаг пропускается.

3. Третий вид - параллельный перенос (сдвиг) вдоль осей ox и oy.

Это преобразование производится в последнюю очередь при наличии коэффициентов a и b, отличных от нуля. При положительном а график сдвигается влево на |а| единиц, при отрицательных а - вправо на |а| единиц. При положительном b график функции параллельно переносим вверх на |b| единиц, при отрицательном b - вниз на |b| единиц.

Рассмотрим примеры

Пример1

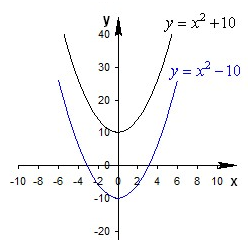
Построить графики функции \(y = {x^2} - 10\) и \(y = {x^2} + 10\) в одной координатной плоскости.

Построим для начала график функции \(y = {x^2}\) , это парабола с вершиной в точке (0;0) и ветвями вверх.

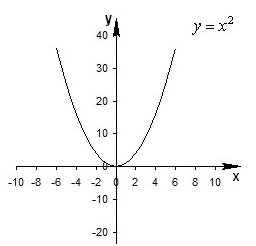
Для построения искомого графика функции \(y = {x^2} - 10\) необходимо параболу параллельно перенести в отрицательном направлении по У, т.е. вниз. Для построения искомого графика функции \(y = {x^2} + 10\) необходимо параболу параллельно перенести в положительном направлении по У, т.е. вверх.

Пример2

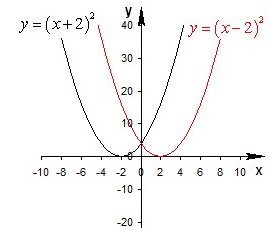
Построить графики функций \(y = {\left( {x + 2} \right)^2}\) и \(y = {\left( {x - 2} \right)^2}\) .

За основу возьмем тот же график параболы, но параллельный перенос будем осуществлять вдоль оси Ох. По правилу переноса график сдвинется влево на 2 единицы для функции \(y = {\left( {x + 2} \right)^2}\) . А для функции \(y = {\left( {x - 2} \right)^2}\) сдвиг произойдет вправо.

Пример3

Построить график функции \(y = - {x^2}\) .

За основу возьмем тот же график параболы. Производимое изменение графика носит название -отображение. Картинка получится симметричной исходной параболе, симметрия относительно Ох.

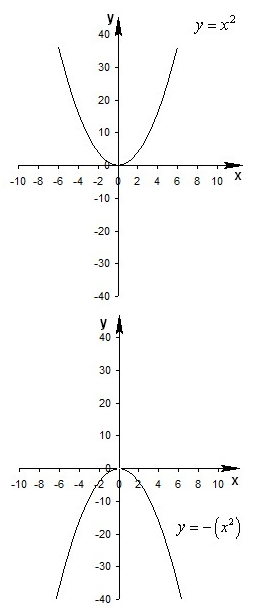
Пример4

Построить графики функций \(y = \left( {3{x^2}} \right)\) и \(y = \left( {\frac{1}{3}{x^2}} \right)\) .

Для построения этих графиков произведем сжатие графика \(y = {x^2}\) для первой функции и растяжение – для второй.