Про монотонность функции, ее наибольшие и наименьшие значения можно прочитать в статье 3.2.1. В данной статье расширим тему и изучим асимптоты функции и их значение.

К об­ла­сти опре­де­ле­ния и зна­че­ния функ­ций имеют от­но­ше­ние такие вспо­мо­га­тель­ные эле­мен­ты гра­фи­ка функ­ций как асимп­то­ты.

Асимп­то­та гра­фи­ка функ­ции - это пря­мая, рас­сто­я­ние от ко­то­рой до гра­фи­ка функ­ции при уда­ле­нии на бес­ко­неч­ность стре­мит­ся к нулю.

Хо­ро­шей на­гляд­ной де­мон­стра­ци­ей асимп­тот яв­ля­ет­ся гра­фик стан­дарт­ной дроб­но-ра­ци­о­наль­ной функ­ции $y = \frac{1}{x}$ , ко­то­рый на­зы­ва­ют ги­пер­бо­лой:

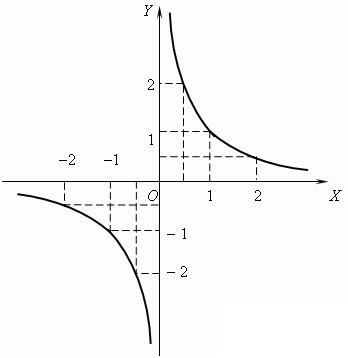
Этот гра­фик де­мон­стри­ру­ет два наи­бо­лее часто встре­ча­ю­щих­ся типа асимп­тот: вер­ти­каль­ную и го­ри­зон­таль­ную. На гра­фи­ке вер­ти­каль­ной асимп­то­той яв­ля­ет­ся ось Оу, ее урав­не­ние х=0 - к ней гра­фик при­жи­ма­ет­ся по вер­ти­ка­ли, а го­ри­зон­таль­ной - ось Ох, ее урав­не­ние у=0 - к ней гра­фик при­жи­ма­ет­ся по го­ри­зон­та­ли.

Уме­ние на­хо­дить асимп­то­ты по­лез­но для по­стро­е­ния гра­фи­ков дроб­но-ра­ци­о­наль­ных и дру­гих функ­ций.

Как видим, асимп­то­та яв­ля­ет­ся пря­мой ли­ни­ей, и для того, что бы ее найти, необ­хо­ди­мо опре­де­лить ее урав­не­ние, т.е. со­от­вет­ству­ю­щую ей функ­цию.

Вер­ти­каль­ная асимп­то­та об­ра­зу­ет­ся в той точке, где зна­че­ние функ­ции стре­мит­ся к бес­ко­неч­но­сти. Это про­ис­хо­дит при ар­гу­мен­тах, при ко­то­рых в функ­ции воз­ни­ка­ет де­ле­ние на ноль.

Го­ри­зон­таль­ная асимп­то­та яв­ля­ет­ся зна­че­ни­ем, к ко­то­ро­му функ­ция стре­мит­ся на бес­ко­неч­но­сти. Для ее опре­де­ле­ния в общем слу­чае необ­хо­ди­мо вво­дить по­ня­тие пре­де­ла, но за­ча­стую в неслож­ных функ­ци­ях до­ста­точ­но про­сто ло­ги­че­ски по­смот­реть, к каким зна­че­ни­ям функ­ция при­бли­жа­ет­ся при уве­ли­че­нии ар­гу­мен­та до $+ \infty$ и при умень­ше­нии до $- \infty$. В ука­зан­ном при­ме­ре с ги­пер­бо­лой неслож­но опре­де­лить и без гра­фи­ка, что при уве­ли­че­нии икса до $+ \infty$ зна­че­ние дроби $\frac{1}{x}$ стре­мит­ся к нулю, то же само про­ис­хо­дит и при умень­ше­нии икса до $- \infty$.

Также существует на­клон­ная асимп­то­та. Наклонные асимптоты традиционно записываются уравнением прямой с угловым коэффициентом $y = kx + b$. Для ее отыскания используют понятие предела и общее правило:

Если существуют два конечных предела $\mathop {\lim }\limits_{x \to \pm \infty } \frac{{f(x)}}{x} = k;\mathop {\lim }\limits_{x \to \pm \infty } \left( {f(x) - kx} \right) = b,$ то прямая $y = kx + b$ является наклонной асимптотой графика функции $y = f(x),x \to \pm \infty .$ Если хотя бы один из перечисленных пределов бесконечен, то наклонная асимптота отсутствует.

Для удоб­ства по­стро­е­ния гра­фи­ков функ­ций рас­смат­ри­ва­ют такую ха­рак­те­ри­сти­ку, как точки пе­ре­се­че­ния с осями.

Точки пе­ре­се­че­ния с осями гра­фи­ка функ­ции - это зна­че­ния ар­гу­мен­та и функ­ции, при ко­то­рых одно из них равно нулю. Нулю могут рав­нять­ся од­но­вре­мен­но и ар­гу­мент с функ­ци­ей, если гра­фик про­хо­дит через на­ча­ло ко­ор­ди­нат.

Для на­хож­де­ния точек пе­ре­се­че­ния гра­фи­ка с осью Оу необ­хо­ди­мо под­ста­вить в функ­цию ну­ле­вое зна­че­ние ар­гу­мен­та, т.е.х=0.

Для на­хож­де­ния точек пе­ре­се­че­ния гра­фи­ка с осью Ох необ­хо­ди­мо ре­шить урав­не­ние f(x)=0. В дан­ном слу­чае удоб­нее упо­треб­лять имен­но обо­зна­че­ние функ­ции f(x), а не y, чтобы под­черк­нуть, что к нулю необ­хо­ди­мо при­рав­нять имен­но фор­му­лу, ко­то­рая за­да­ет функ­цию, а не про­сто игрек.

Пример

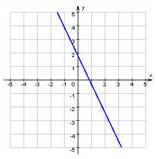
Для ли­ней­ной функ­ции $y = f(x) = 2 - 2x$ точка пе­ре­се­че­ния с осью Оу имеет ко­ор­ди­на­ты х=0 и $y = 2 - 2 \cdot 0 = 2$ . Точка пе­ре­се­че­ния с осью Ох имеет ко­ор­ди­на­ты:

$\begin{gathered} 2 - 2x = 0 \Rightarrow 2x = 2 \Rightarrow x = 1; \\ y = 0. \\ \end{gathered}$

 График: