Математика
2.2.9. Метод интервалов
Решение неравенств методом интервалов
Этот метод решения неравенств достаточно универсален, важно помнить, что не всегда применение данного метода оправдано с точки зрения объема вычислений. Иногда бывает удобнее воспользоваться некоторыми другими методами решения неравенств.
Пусть заданное неравенство имеет вид: \(\frac{{f(x)}}{{g(x)}} < , > , \leqslant , \geqslant 0.\)Для решения этого неравенства используется так называемый метод интервалов (метод промежутков), который состоит в следующем:
Во-первых, на числовую ось наносят точки \({x_1},...,{x_n},\)разбивающие ее на промежутки, в которых выражение \(\frac{{f(x)}}{{g(x)}}\) определено и сохраняет знак («плюс» или «минус»). Такими точками могут быть корни уравнений \(f(x) = 0\) и \(g(x) = 0\) . Соответствующие этим корням точки отмечают на числовой оси: закрашенными кружками - точки, удовлетворяющие заданному неравенству, а светлыми кружками - не удовлетворяющие ему.
Во-вторых, определяют и отмечают на числовой оси знак выражения \(\frac{{f(x)}}{{g(x)}}\) для значений, принадлежащих каждому из полученных промежутков. Если функции \(f(x) = 0\) и \(g(x) = 0\) являются многочленами и не содержат множителей вида \({(x - a)^{2n}},\)где \(n \in N,\) то достаточно определить знак функции \(\frac{{f(x)}}{{g(x)}}\)в любом таком промежутке, а в остальных промежутках знаки «плюс» и «минус» будут чередоваться.
Если же в числителе или знаменателе дроби \(\frac{{f(x)}}{{g(x)}}\) имеется множитель вида \({(x - a)^{2n}},\) где \(n \in N,\) то непосредственной проверкой выясняют, удовлетворяет ли значение, равное а, заданному неравенству.
Изменение знаков удобно иллюстрировать с помощью волнообразной кривой (кривой знаков), проведенной через отмеченные точки и лежащей выше или ниже числовой оси в соответствии со знаком дроби \(\frac{{f(x)}}{{g(x)}}\) в рассматриваемом промежутке. Промежутки, которые содержат точки, удовлетворяющие данному неравенству, иногда покрывают штрихами. На ту же ось помещают и точки, соответствующие \(x = a\). Заштрихованная область в совокупности с полученными точками будет являться ответом к неравенству.
Пример
Решите неравенство:
\(\frac{1}{{{x^2} - 5x + 6}} \leqslant \frac{1}{2}.\)
Решение.
Перенесем 1/2 в левую часть и приведем все к общему знаменателю:
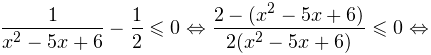
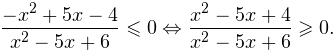
Выражения, стоящие в числителе и знаменателе, можно разложить на множители, тогда неравенство примет вид:

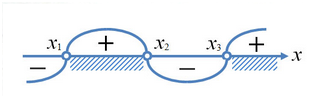
Далее по алгоритму решения неравенств методом интервалов находим корни уравнений (х-4)(х-1)=0 и (х-2)(х-3)=0. Из первого получаем \({x_1} = 4,{x_2} = 1.\) Из второго получаем \({x_3} = 2,{x_4} = 3.\) Наносим на числовую прямую получившиеся точки, причем точки х1 и х2 обозначаем закрашенными кружочками (для них неравенство выполняется), а точки х3 и х4 - светлыми (для них неравенство не выполняется, при этих значениях, выражение, стоящее слева от знака неравенства, вообще не имеет смысла):
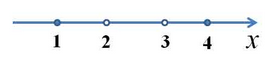
Определяем теперь знаки выражения на полученных промежутках (подставляем любое значение хиз каждого полученного промежутка в данное выражение), изображаем кривую знаков, заштриховываем те промежутки, на которых исходное неравенство выполняется:
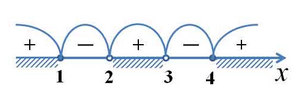
Итак, исходному неравенству удовлетворяют следующие значения:
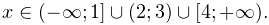
Другие материалы по данной теме
Видео
3.5. Примеры решения задач