Процессы, возникающие в электрических цепях под действием внешнего периодического источника тока, называются вынужденными колебаниями.

Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Внешний источник периодического воздействия обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь.

Особый интерес представляет случай, когда внешний источник, напряжение которого изменяется по гармоническому закону с частотой ω, включен в электрическую цепь, способную совершать собственные свободные колебания на некоторой частоте ω₀.

Если частота ω₀ свободных колебаний определяется параметрами электрической цепи, тоустановившиеся вынужденные колебания всегда происходят на частоте ω внешнего источника.

Для установления вынужденных стационарных колебаний после включения в цепь внешнего источника необходимо некоторое время Δt. Это время по порядку величины равно времени \(\tau \) затухания свободных колебаний в цепи.

Электрические цепи, в которых происходят установившиеся вынужденные колебания под действием периодического источника тока, называются цепями переменного тока.

Рассмотрим последовательный колебательный контур, то есть RLC-цепь, в которую включен источник тока, напряжение которого изменяется по периодическому закону: e (t) = ℰ₀ cos ωt, где ℰ₀ – амплитуда, ω – круговая частота.

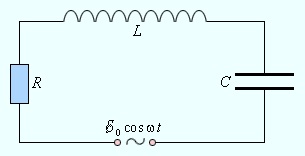
Предполагается, что для электрической цепи, изображенной на рис. 2.3.1, выполнено условие квазистационарности. Поэтому для мгновенных значений токов и напряжений можно записать закон Ома: \(RJ + \frac{q}{C} + L\frac{{dJ}}{{dt}} = {{\cal E}_{\bf{0}}}\)cosωt.

Величина \(L\frac{{dJ}}{{dt}}\) – это ЭДС самоиндукции катушки, перенесенная с изменением знака из правой части уравнения в левую. Эту величину принято называть напряжением на катушке индуктивности.

Уравнение вынужденных колебаний можно записать в виде u_R + u_C + u_L = e (t) = ℰ₀ cos ωt, где u_R (t), u_C (t) и u_L (t) – мгновенные значения напряжений на резисторе, конденсаторе и катушке соответственно. Амплитуды этих напряжений будем обозначать буквами U_R, U_C и U_L. При установившихся вынужденных колебаниях все напряжения изменяются с частотой ω внешнего источника переменного тока. Для наглядного решения уравнения вынужденных колебаний можно использовать метод векторных диаграмм.

На векторной диаграмме колебания определенной заданной частоты ω изображаются с помощью векторов. Ниже изображение гармонических колебаний A cos (ωt + φ₁), B cos (ωt + φ₂) и их суммы C cos (ωt + φ) с помощью векторов на векторной диаграмме.

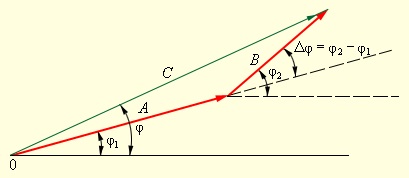
Длины векторов на диаграмме равны амплитудам A и B колебаний, а наклон к горизонтальной оси определяется фазами колебаний φ₁ и φ₂. Взаимная ориентация векторов определяется относительным фазовым сдвигом Δφ = φ₁ – φ₂. Вектор, изображающий суммарное колебание, строится на векторной диаграмме по правилу сложения векторов: C⃗ =A⃗ +B⃗ .

Для того, чтобы построить векторную диаграмму напряжений и токов при вынужденных колебаниях в электрической цепи, нужно знать соотношения между амплитудами токов и напряжений и фазовый сдвиг между ними для всех участков цепи.

Рассмотрим по отдельности случаи подключения внешнего источника переменного тока к резистру с сопротивлением R, конденсатору с емкостью C и катушки с индуктивностью L. Во всех трех случаях напряжение на резисторе, конденсаторе и катушке равно напряжению источника переменного тока.

Резистор в цепи переменного тока \({J_R}R = {u_R} = {U_R}\cos \omega t;\)\({J_R} = \frac{{{U_R}}}{R}\cos \omega t = {I_R}\cos \omega t.\)

Здесь через I_R обозначена амплитуда тока, протекающего через резистор. Связь между амплитудами тока и напряжения на резисторе выражается соотношением RI_R = U_R.

Фазовый сдвиг между током и напряжением на резисторе равен нулю.

Физическая величина R называется активным сопротивлением резистора.