Расстояние между оптическим центром линзыO и главным фокусом F называется фокусным расстоянием. Оно обозначаетcя буквой F.

Положение изображения и его характер (действительное или мнимое) можно также рассчитать с помощью формулы тонкой линзы. Расстояние от предмета до линзы обозначить через d, а расстояние от линзы до изображения через f.

Величину D, обратную фокусному расстоянию. называют оптической силой линзы. Единицой измерения оптической силы является диоптрия (дптр). Диоптрия – оптическая сила линзы с фокусным расстоянием 1 м: 1 дптр = м^–1. Формула тонкой линзы аналогична формуле сферического зеркала. 

Фокусным расстояниям линз принято приписывать определенные знаки: для собирающей линзы F > 0, для рассеивающей F < 0.

Величины d и f также подчиняются определенному правилу знаков: 
d > 0 и f > 0 – для действительных предметов (то есть реальных источников света, а не продолжений лучей, сходящихся за линзой) и изображений; 
d < 0 и f < 0 – для мнимых источников и изображений.

В зависимости от положения предмета по отношению к линзе изменяются линейные размеры изображения. Линейным увеличением линзы Γ называют отношение линейных размеров изображения h' и предмета h. Величине h', как и в случае сферического зеркала, удобно приписывать знаки плюс или минус в зависимости от того, является изображение прямым или перевернутым. Величина h всегда считается положительной. Поэтому для прямых изображений Γ > 0, для перевернутых Γ < 0. Из подобия треугольников на рисунке ниже легко получить формулу для линейного увеличения тонкой линзы:Γ=h'h=-fd.

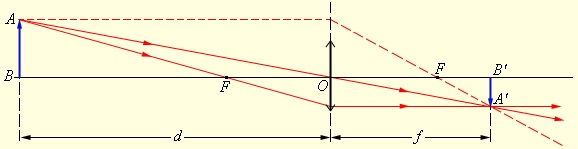
В рассмотренном примере с собирающей линзой: d = 3F > 0, f=32F>0;следовательно, Γ=-12<0 – изображение перевернутое и уменьшенное в 2 раза.

В примере с рассеивающей линзой: d = 2|F| > 0, f=-23|F|<0; следовательно, Γ=13>0 – изображение прямое и уменьшенное в 3 раза.

Оптическая сила D линзы зависит как от радиусов кривизны R₁ и R₂ ее сферических поверхностей, так и от показателя преломления n материала, из которого изготовлена линза. В курсах оптики доказывается следующая формула: \(D = \frac{1}{F} = \left( {n - 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)\).

Радиус кривизны выпуклой поверхности считается положительным, вогнутой – отрицательным. Эта формула используется при изготовлении линз с заданной оптической силой.

Во многих оптических приборах свет последовательно проходит через две или несколько линз. Изображение предмета, даваемое первой линзой, служит предметом (действительным или мнимым) для второй линзы, которая строит второе изображение предмета. Это второе изображение также может быть действительным или мнимым. Расчет оптической системы из двух тонких линз сводится к двукратному применению формулы линзы, при этом расстояние d₂ от первого изображения до второй линзы следует положить равным величине l – f₁, где l – расстояние между линзами. Рассчитанная по формуле линзы величина f₂ определяет положение второго изображения и его характер (f₂ > 0 – действительное изображение, f₂ < 0 – мнимое). Общее линейное увеличение Γ системы из двух линз равно произведению линейных увеличений обеих линз: Γ = Γ₁ ċ Γ₂. Если предмет или его изображение находятся в бесконечности, то линейное увеличение утрачивает смысл.

Частным случаем является телескопический ход лучей в системе из двух линз, когда и предмет, и второе изображение находятся на бесконечно больших расстояниях. Телескопический ход лучей реализуется в зрительных трубах – астрономической трубе Кеплера и земной трубе Галилея.

Тонкие линзы обладают рядом недостатков, не позволяющих получать высококачественные изображения. Искажения, возникающие при формировании изображения, называются аберрациями. Главные из них – сферическая и хроматическая аберрации. Сферическая аберрация проявляется в том, что в случае широких световых пучков лучи, далекие от оптической оси, пересекают ее не в фокусе. Формула тонкой линзы справедлива только для лучей, близких к оптической оси. Изображение удаленного точечного источника, создаваемое широким пучком лучей, преломленных линзой, оказывается размытым.

Хроматическая аберрация возникает вследствие того, что показатель преломления материала линзы зависит от длины волны света λ. Это свойство прозрачных сред называется дисперсией. Фокусное расстояние линзы оказывается различным для света с разными длинами волн, что приводит к размытию изображения при использовании немонохроматического света.

В современных оптических приборах применяются не тонкие линзы, а сложные многолинзовые системы, в которых удается приближенно устранить различные аберрации.

Формирование собирающей линзой действительного изображения предмета используется во многих оптических приборах, таких как фотоаппарат, проектор и т. д.