Физика
3.2.6. Закон Ома для полной (замкнутой) электрической цепи
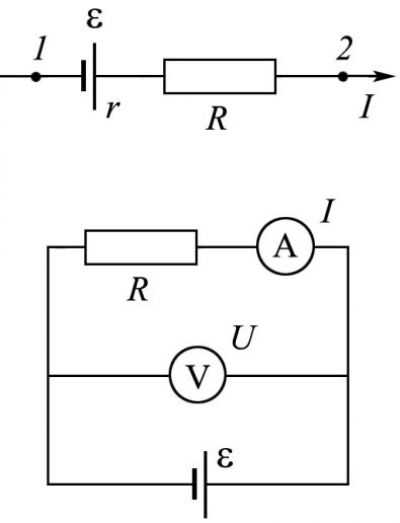
Закон Ома для полной цепи. Закон Ома для цепи, содержащей ЭДС (неоднородный участок цепи)
Теорема физики (формула) и словесная формулировка математической записи: ток на участке цепи I, содержащем ЭДС ε, равен сумме разности потенциалов на этом участке φ1 − φ2 и ЭДС источника ε, деленной на общее сопротивление участка R: \(I = \frac{{{\varphi _{\rm{1}}} - {\varphi _{\rm{2}}} + {\rm{\varepsilon }}}}{R}\),
причем R= R1 + r, где r − внутреннее сопротивление источника ЭДС, а R1 − суммарное сопротивление остальных элементов участка. ЭДС ε берется со знаком «плюс», если ток, создаваемый ЭДС, течет так же, как ток участка, и со знаком «минус», если в противоположную сторону.
Доказательство теоремы. Вывод формулы: докажем теорему с помощью закона сохранения энергии. Работа электрических и сторонних сил по перемещению заряда на участке А равна изменению электрической энергии ∆W, и, если провода и другие элементы участка остаются неподвижны, то вся эта энергия переходит в джоулево тепло Q: Q =∆W;Q = А. (1)
А = q·ε + q·(φ1 − φ2), а Джоулево тепло Q = I2Rt = IR·It = IR·q (здесь использовано определение постоянного тока I = q/t). Подставляя в (1) значения величин и сокращая на q, придем к искомой формуле:
q·ε +q(φ1 − φ2) =IR·q → \(I = \frac{{{\varphi _1} - {\varphi _2} + {\rm{\varepsilon }}}}{R}\).
При выводе учтено, что тепловые потери присутствуют и внутри источника ЭДС, т.е. R= R1 + r, где r − внутреннее сопротивление источника ЭДС, а R1 − суммарное сопротивление остальных элементов выбранного участка.
Следствия:
1. Если участок не содержит ЭДС (ε = 0), формула совпадает с законом Ома для участка цепи, не содержащего ЭДС:
\(I = \frac{{{\varphi _1} - {\varphi _2}}}{R} = \frac{U}{R}\)
2. Для полной цепи точка 1 совпадает с точкой 2: φ1 − φ2 = 0, и получаем закон Ома для полной цепи: \(I = \frac{{\rm{\varepsilon }}}{{R + r}}\),
где r – внутреннее сопротивление источника, а R – сопротивление остальных элементов цепи.
Условия выполнения: поскольку при выводе использовано следствие из закона Джоуля–Ленца, основанное на законе Ома, то формула выполняется тогда же, когда и закон Ома: для проводников (металлов) и полупроводников в интервале температур от превышающих температуры сверхпроводимости до температуры плавления. Кроме того, элементы цепи не должны совершать механических движений и не должно происходить других видов потерь энергии.
Другие материалы по данной теме
Формула
\(I = \frac{E}{{R + r}}\)
Видео
5.9. Закон Ома для полной цепи