Функция \(y=log_a x,\), где \(x>0,a>0,a \neq 1,\), называется логарифмической. Число c называется логарифмом числа b > 0 по основанию \(a>0,a \neq 1,\), если \(a^c=b.\)Обозначается \(c=log_a b,a>0,a \neq 1,b>0.\) Отсюда следует основное логарифмическое тождество:

\(a^{log_a b}=b.\)

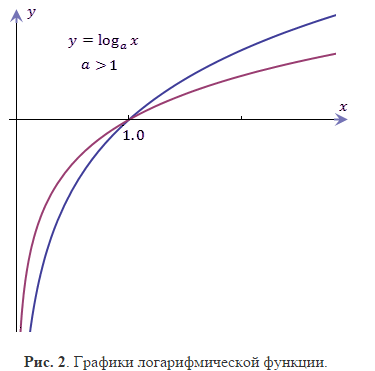
Показательная и логарифмическая функции с одинаковыми основаниями являются взаимно обратными.
Областью значения логарифмической функции является вся числовая ось, причём \(\forall y \in R\) найдётся только один x > 0, на котором y достигается.
 Если a > 1, то \(y=log_a x,\) возрастает;
 если 0<a<1, то \(y=log_a x,\) убывает.