Об­ласть зна­че­ний функ­ции - это мно­же­ство зна­че­ний функ­ции, ко­то­рые она при­ни­ма­ет в своей об­ла­сти опре­де­ле­ния. Т.е. в стан­дарт­ной за­пи­си функ­ции это зна­че­ния ее иг­ре­ка. Мно­же­ство зна­че­ний функ­ции при­ня­то обо­зна­чать E или E(y).

За­да­ча на опре­де­ле­ние мно­же­ства зна­че­ний функ­ции, как пра­ви­ло, более слож­на, чем за­да­ча на поиск об­ла­сти опре­де­ле­ния. Дело в том, что в таком слу­чае необ­хо­ди­мо ис­кать не огра­ни­че­ния на ариф­ме­ти­че­ские дей­ствия, а мно­же­ство всех ре­зуль­та­тов этих дей­ствий, а это непро­сто.

Рас­смот­рим ос­нов­ные под­хо­ды к ре­ше­нию в дан­ном слу­чае.

1) Для функ­ций, за­дан­ных ана­ли­ти­че­ски, для по­ис­ка об­ла­сти зна­че­ний можно ис­поль­зо­вать метод на­хож­де­ния об­рат­ной функ­ции, но этот спо­соб не самый про­стой и не все функ­ции од­но­знач­но об­ра­ти­мы. Для неслож­ных при­ме­ров, обыч­но до­ста­точ­но поль­зо­вать­ся за­ра­нее из­вест­ны­ми об­ла­стя­ми зна­че­ний про­стей­ших функ­ций. Пе­ре­чис­лим такие самые часто встре­ча­ю­щи­е­ся функ­ции:

1. Вы­ра­же­ния, ко­то­рые воз­во­дят­ся в чет­ные сте­пе­ни, все­гда неот­ри­ца­тель­ны. На­при­мер, \(y = {x^2} \geqslant 0\) или \(y = {\left( {x - 1} \right)^{10}} \geqslant 0\). Для этих функций область значений \(E(y) = [0; + \infty ).\)

На нечет­ные сте­пе­ни ука­зан­ное свой­ство не рас­про­стра­ня­ет­ся!!

2. Функ­ции, ко­то­рые пред­став­ля­ют собой корни чет­ных сте­пе­ней, также все­гда имеют неот­ри­ца­тель­ные зна­че­ния. На­при­мер, \(y = \sqrt x \geqslant 0\) или \(y = \sqrt[4]{{{x^3} - 8}} \geqslant 0\) , для них об­ла­стью зна­че­ний яв­ля­ет­ся \(E(y) = [0; + \infty ).\).

На нечет­ные корни ука­зан­ное свой­ство не рас­про­стра­ня­ет­ся!!

3. Квад­ра­тич­ная функ­ция тоже имеет огра­ни­чен­ную об­ласть зна­че­ний. Это удоб­но уви­деть на гра­фи­ке, изоб­ра­зим, на­при­мер, гра­фик функ­ции \(y = - 2{x^2} + 12x - 10\) . Вос­поль­зо­вав­шись, к при­ме­ру, ме­то­дом опре­де­ле­ния вер­ши­ны па­ра­бо­лы, по­лу­чим такой гра­фик:

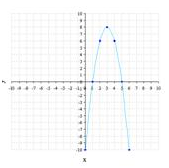
Коэффициент а в квадратном уравнении меньше 0, равен -2, т.о. ветки параболы направлены вверх. Мак­си­маль­ное зна­че­ние равно 8, а все осталь­ные зна­че­ния мень­ше. Таким об­ра­зом, об­ласть зна­че­ний этой функ­ции \(E(y) = ( - \infty ;8].\) Для того чтобы по­лу­чить этот ответ не обя­за­тель­но ри­со­вать гра­фик, до­ста­точ­но про­сто уметь на­хо­дить ко­ор­ди­на­ту вер­ши­ны па­ра­бо­лы по оси ор­ди­нат и пом­нить, что при по­ло­жи­тель­ном стар­шем ко­эф­фи­ци­ен­те функ­ции, ее ветки на­прав­ле­ны вверх, а при от­ри­ца­тель­ном вниз.

Таким об­ра­зом, можно сфор­му­ли­ро­вать ал­го­ритм по­ис­ка об­ла­сти зна­че­ний квад­ра­тич­ной функ­ции: на­хо­дим иг­ре­ко­вую ко­ор­ди­на­ту ее вер­ши­ны и учи­ты­ва­ем на­прав­ле­ние веток па­ра­бо­лы по знаку стар­ше­го ко­эф­фи­ци­ен­та, т.е. мно­жи­те­ля при х².

4. По­ка­за­тель­ная функ­ция все­гда при­ни­ма­ет по­ло­жи­тель­ные зна­че­ния. На­при­мер, \(y = {5^x} > 0,\)для нее \(E(y) = (0; + \infty ).\)

5. Такие три­го­но­мет­ри­че­ские функ­ции как синус и ко­си­нус имеют двух­сто­рон­ние огра­ни­че­ния по об­ла­сти зна­че­ний. Их зна­че­ния огра­ни­че­ны про­ме­жут­ком \(E(y) = [ - 1;1].\)

Это легко увидеть по графикам:

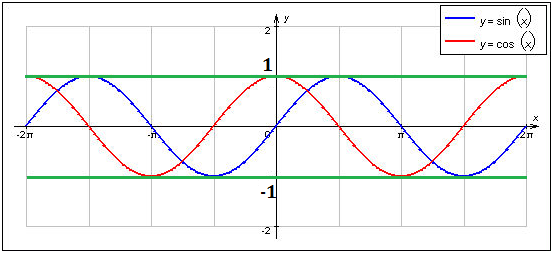
При ре­ше­нии задач на опре­де­ле­ние об­ла­сти зна­че­ний функ­ции необ­хо­ди­мо уметь ис­поль­зо­вать ука­зан­ные огра­ни­че­ния на ос­нов­ные про­стей­шие функ­ции и пре­об­ра­зо­вы­вать их.

2) Для таб­лич­но­го спо­со­ба за­да­ния функ­ции на­хож­де­ние об­ла­сти зна­че­ний так же эле­мен­тар­но, как и об­ла­сти опре­де­ле­ния. Для этого про­сто до­ста­точ­но пе­ре­чис­лить все ука­зан­ные в таб­ли­це зна­че­ния функ­ции.

3) В слу­чае гра­фи­че­ско­го спо­со­ба за­да­ния функ­ции об­ласть зна­че­ний видна по гра­фи­ку, как и об­ласть опре­де­ле­ния. В дан­ном слу­чае необ­хо­ди­мо ука­зы­вать мно­же­ство всех зна­че­ний ко­ор­ди­нат точек гра­фи­ка по оси ор­ди­нат, т.е. всех иг­ре­ков.

Пример:

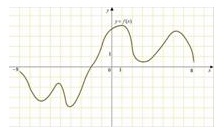
Область значений данной функции ограничена сверху числом 4 и снизу числом -4, т.о.

\(E(y) = [ - 4;4].\)