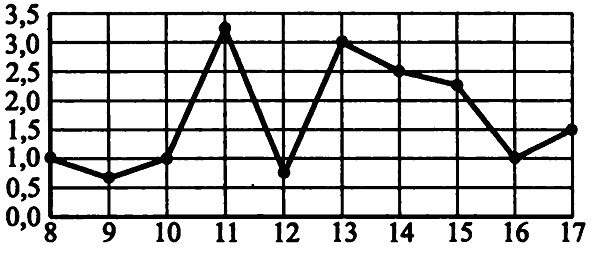
На рисунке жирными точками показано суточное количество осадков, выпавших в Томске с 8 по 17 сентября 2012 года. По горизонтали указаны числа сентября, по вертикали – количество осадков, выпавших в соответствующий день (в миллиметрах). Для наглядности точки соединены на рисунке линией. Определите по рисунку, в какой день сентября выпало ровно 2,5 мм осадков.