Гелий и аргон можно опи­сы­вать мо­де­лью иде­аль­но­го од­но­атом­но­го газа, для ко­то­ро­го при­ме­ни­мо урав­не­ние Кла­пей­ро­на–Мен­де­ле­е­ва \(PV=\nu RT\). Пор­шень в ци­лин­дре вна­ча­ле на­хо­дит­ся в со­сто­я­нии ме­ха­ни­че­ско­го рав­но­ве­сия, так что дав­ле­ния газов в на­чаль­ный мо­мент сов­па­да­ют. То же самое можно ска­зать и про ко­неч­ный мо­мент вре­ме­ни. В на­чаль­ный мо­мент объёмы газов оди­на­ко­вы и равны 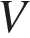, и урав­не­ние Кла­пей­ро­на–Мен­де­ле­е­ва при­во­дит к связи между на­чаль­ны­ми тем­пе­ра­ту­ра­ми гелия и ар­го­на \(T_{1}\)  и \(T_{2}\) и чис­лом молей этих газов \(\nu _{1}\)  и \(\nu _{2}\): \(\nu _{1}T_{1}=\nu _{2}T_{2}\).

После уста­нов­ле­ния теп­ло­во­го рав­но­ве­сия тем­пе­ра­ту­ра газов равна \(T\), а объёмы гелия и ар­го­на из­ме­ни­лись и стали равны \(V_{1}\) и \(V_{2}\) со­от­вет­ствен­но. Урав­не­ния Кла­пей­ро­на–Мен­де­ле­е­ва, записанные для состояний газов в этот мо­мент, при­во­дят к со­от­но­ше­нию \(\frac{V_{1}}{V_{2}}=\frac{\nu _{1}}{\nu _{2}}\). По­сколь­ку сум­мар­ный объём ци­лин­дра остал­ся не­из­мен­ным, можно записать: \(V_{1}+V_{2}=2V\). Тогда по­лу­ча­ем, что \(\frac{V_{1}}{V}=\frac{2}{1+\frac{\nu _{2}}{\nu _{1}}}\). Учи­ты­вая, что \(\frac{\nu _{2}}{\nu _{1}}=\frac{T _{1}}{T _{2}}\)  , по­лу­чим \(\frac{V_{1}}{V}=2\frac{T_{2}}{T_{1}+T_{2}}=\frac{3}{2}=1,5\).