Определим фокусное расстояние линзы:

\(F=\frac{1}{D}=\frac{1}{5}=0,2\)м.

Используя формулу тонкой линзы, определим, на каком расстоянии от линзы будет располагаться объект:

\(\frac{1}{F}=\frac{1}{d}+\frac{1}{f} \Leftrightarrow f=\frac{Fd}{d-F}\).

Из рисунка видно, используя подобие треугольников, что высота изображения карандаша h связана с высотой самого карандаша H и расстояниями f и d соотношением:

\(h=H\frac{f}{d}=\frac{HF}{d-F}=\frac{0,09\cdot 0,2}{0,5-0,2}=0,06\)(м).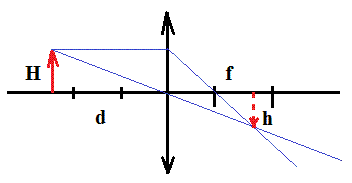

Правильный ответ: 0,06 м.