Математика
2.2.4. Логарифмические неравенства
Логарифмические неравенства
При решении уравнений и неравенств с логарифмами используются переходы к системам и совокупностям равносильных условий, что упрощает последовательность преобразований, а также упрощает нахождение области допустимых значений переменной.
При решении простейшего логарифмического неравенства \(log_af(x)>log_ag(x)\) при \(a>0,a\neq1\) возможны два случая:
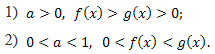
Логарифмические неравенства с переменным основанием:
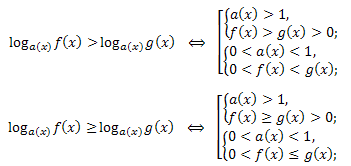
Имеет место важная
Теорема 2: Знак логарифма \(log_{a(x)}f(x)\) совпадает со знаком произведения \((a(x)-1)(f(x)-1)\) в области допустимых значений.
Тогда имеют место следующие равносильности:
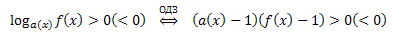
или полное условие равносильности, включающее ОДЗ:
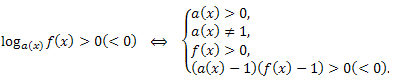
Для нестрогих неравенств:
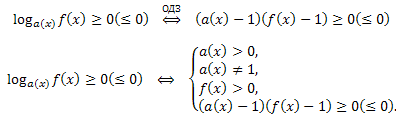
Теорема 3: Знак разности \(log_{a(x)}f(x)-log_{a(x)}g(x)\) совпадает со знаком произведения \((a(x)-1)(f(x)-g(x))\) в области допустимых значений.
Отсюда следуют равносильные переходы в неравенствах:
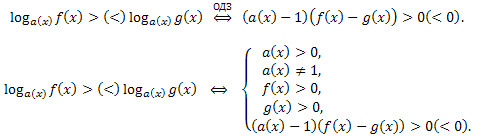
Для нестрогих неравенств:
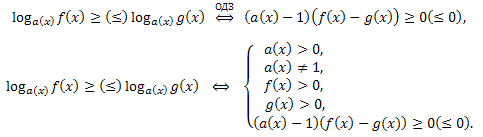
Следствие:
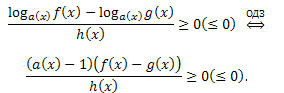
Другие материалы по данной теме
Видео
5.6.Логарифмические неравенства
