Удельной энергией связи ядра w_св называется энергия связи, приходящаяся на один нуклон:

\({w_{{\rm с}{\rm в}}} = \frac{{{E_{{\rm с}{\rm в}}}}}{A}\).

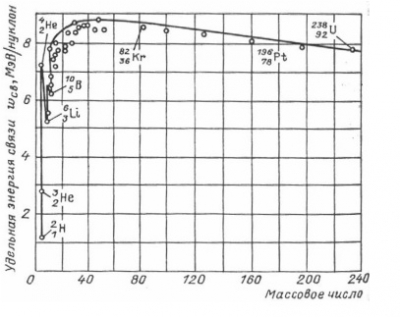
Величина w_св составляет в среднем 8 МэВ/нуклон. На рисунке приведена кривая зависимости удельной энергии связи от массового числа A, характеризующая различную прочность связей нуклонов в ядрах разных химических элементов. Ядра элементов в средней части периодической системы (\(28 < A < 138\)), т.е. от \({}_{14}^8{\rm{Si}}\) до \({}_{{\rm{50}}}^{{\rm{38}}}{\rm{Ba}}\), наиболее прочны.

В этих ядрах w_св близка к 8,7 МэВ/нуклон. По мере увеличения числа нуклонов в ядре удельная энергия связи убывает. Ядра атомов химических элементов, расположенных в конце периодической системы (например, ядро урана), имеют w_св ≈ 7,6 МэВ/нуклон. Это объясняет возможность выделения энергии при делении тяжелых ядер.

В области малых массовых чисел имеются острые «пики» удельной энергии связи. Максимумы характерны для ядер с четными числами протонов и нейтронов (\({}_2^4{\rm{He}}\), \({}_6^{12}{\rm{C}}\), \({}_8^{16}{\rm{O}}\)), минимумы – для ядер с нечетными количествами протонов и нейтронов (\({}_3^6{\rm{Li}}\), \({}_5^{10}{\rm{B}}\), \({}_7^{14}{\rm{N}}\)).

Если ядро имеет наименьшую возможную энергию \({E_{\min }} = - {E_{{\rm с}{\rm в}}}\),

то оно находится восновном энергетическом состоянии. Если ядро имеет энергию \(E > {E_{\min }}\), то оно находится ввозбужденном энергетическом состоянии. Случай Е = 0 соответствует расщеплению ядра на составляющие его нуклоны. В отличие от энергетических уровней атома, раздвинутых на единицы электронвольт, энергетические уровни ядра отстоят друг от друга на мегаэлектронвольт (МэВ). Этим объясняется происхождение и свойства гамма-излучения.

Критерием устойчивости атомных ядер является соотношение между числом протонов и нейтронов в устойчивом ядре для данных изобар (\(A = {\rm{const}}\)). Условие минимума энергии ядра приводит к следующему соотношению между Z_уст и А:

\({Z_{{\rm у}{\rm с}{\rm т}}} = \frac{A}{{1,98 + 0,015{A^{2/3}}}}\).

Берется ближайшее целое число Z_уст.

При малых и средних значениях А числа нейтронов и протонов в устойчивых ядрах примерно одинаковы: Z ≈ А – Z.

С ростом Z силы кулоновского отталкивания протонов растут пропорционально Z·(Z – 1) ~ Z² (парное взаимодействие протонов), и для компенсации этого отталкивания ядерным притяжением число нейтронов должно возрастать быстрее числа протонов.