Закон о равнораспределении энергии по степеням свободы утверждает, если система частиц находится в состоянии термодинамического равновесия, то средняя кинетическая энергия хаотического движения молекул, приходящаяся на одну степень свободы поступательного
и вращательного движения, равна \(\frac{1}{2}kT.\)

Следовательно, молекула, имеющая 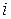 степеней свободы, обладает энергией

\({\overline E _{к\rm{}}} = \frac{i}{2}kT\), (11.2)

где \(k\) – постоянная Больцмана; \(T\) – абсолютная температура газа.

Внутренняя энергия \(U\) идеального газа – это сумма кинетических энергий всех его молекул.

Находим внутреннюю энергию 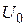 одного моля идеального газа: 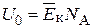, где 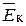 – средняя кинетическая энергия одной молекулы газа,  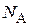– число Авогадро (число молекул в одном моле). Постоянная Больцмана \(k = \frac{R}{{{N_{\rm{A}}}}}\). Тогда

\({U_0} = {\overline E _{к\rm{}}}{N_{\rm{A}}} = \frac{i}{2}kT{N_{\rm{A}}} = \frac{i}{2}\frac{R}{{{N_{\rm{A}}}}}T{N_{\rm{A}}} = \frac{i}{2}RT\).

Если газ имеет массу \(m\), то \(\frac{m}{\mu }\) – число молей, где \({\mu }\) – масса моля, и внутренняя энергия газа выражается формулой

\(U = \frac{m}{{\rm{\mu }}}\frac{i}{2}RT\). (11.3)

Внутренняя энергия идеального газа зависит только от температуры газа. Изменение внутренней энергии идеального газа определяется изменением температуры и не зависит от процесса, при котором это изменение произошло.

Изменение внутренней энергии идеального газа

\(\Delta U = \frac{m}{{\rm{\mu }}}\frac{i}{2}R\Delta T\), (11.4)

где \(\Delta T\) – изменение температуры.

Закон равномерного распределения энергии распространяется на колебательное движение атомов в молекуле. На колебательную степень свободы приходится не только кинетическая энергия, но и потенциальная, причём среднее значение кинетической энергии, приходящейся на одну степень, равно среднему значению потенциальной энергии, приходящемуся на одну степень свободы.

Следовательно, если молекула имеет число степеней свободы
i = i_{поступат} + i_вращат + i_колеб, то средняя суммарная энергия молекулы \(\frac{i}{2}kT\), а внутренняя энергия газа массы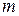

\(U = \frac{m}{\mu }\frac{i}{2}RT\). (11.5)