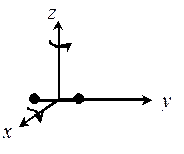Числом степеней свободыназывается наименьшее число независимых координат, которое необходимо ввести, чтобы определить положение тела в пространстве.

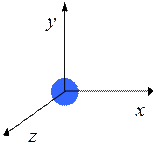
Рассмотрим одноатомный газ. Молекулу такого газа можно считать материальной точкой, положение материальной точки \(M\) (рис. 11.1) в пространстве определяется тремя координатами.

Молекула может двигаться в трех направлениях (рис. 11.2).

Следовательно, молекула газа обладает тремя поступательными степенями свободы.

Молекула – материальная точка. Энергия вращательного движения \(\frac{{I{\omega ^2}}}{2} = 0\), т.к. момент инерции материальной точки относительно оси, проходящей через точку, равен нулю: \({I} = 0\)

Для молекулы одноатомного газа число степеней свободы\(i = {3}\).

Рассмотрим двухатомный газ. В двухатомной молекуле каждый атом принимается за материальную точку и считается, что атомы жёстко связаны между собой, это гантельная модель двухатомной молекулы. Двухатомная жестко связанная молекула – совокупность двух материальных точек, связанных недеформируемой связью (рис. 11.3).

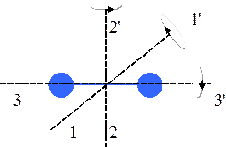
Положение центра масс молекулы задаётся тремя координатами, (рис. 11.4), это три степени свободы, они определяют поступательное движение молекулы. Но молекула может совершать и вращательные движения вокруг осей \({oz}\) и \({ox}\), это ещё две степени свободы, определяющие вращение молекулы. Вращение молекулы вокруг оси \({oy}\) невозможно, т.к. материальные точки не могут вращаться вокруг оси, проходящей через эти точки.

Для молекулы двухатомного газа число степеней свободы\(i = {5}\).