Рассмотрим окружность радиуса 1 с центром в начале координат. Если для координат точки M₁, лежащей на этой окружности, ввести обозначение М₁=(x₁;y₁), то по теореме Пифагора:

\(x_1^2 + y_1^2 = 1.\)

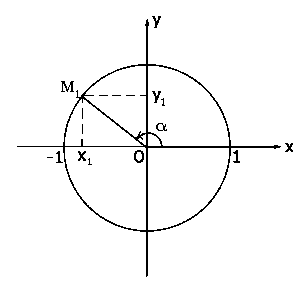
А синус, косинус, тангенс и котангенс угла α будут вычисляться по формулам:

\(\begin{gathered} \sin \alpha = {y_1}, \\ \cos \alpha = {x_1}, \\ tg\alpha = \frac{{{y_1}}}{{{x_1}}}, \\ ctg\alpha = \frac{{{x_1}}}{{{y_1}}}. \\ \end{gathered} \)

Из этих формул, в частности, вытекает основное тригонометрическое тождество:

\({\sin ^2}\alpha + {\cos ^2}\alpha = 1.\)

Таким образом, основное тригонометрическое тождество является теоремой Пифагора, сформулированной с помощью тригонометрических функций.

Окружность радиуса 1, изображенную на рисунке, называют тригонометрическим кругом или числовой окружностью. 

Знаки тригонометрических функций на окружности

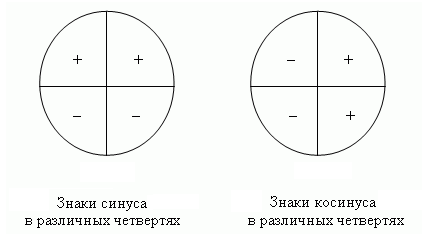
Линия синуса угла - это вертикальный диаметр единичного круга, линия косинуса угла - это горизонтальный диаметр единичного круга. Таким образом, можно рассуждать о знаках этих тригонометрических функций. Знаки синуса и косинуса в различных четвертях единичного круга показаны на рисунке:

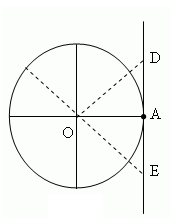
Линия тангенса - это касательная к единичному кругу, проведенная через точку A горизонтального диаметра.

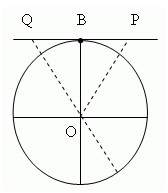
Линия котангенса - это касательная к единичному кругу, проведенная через точку В вертикального диаметра.

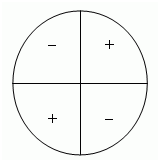
Знаки тангенса и котангенса одинаковы для четвертей окружности, их можно выучить по рисунку: