Математика
1.2.1. Синус, косинус, тангенс, котангенс произвольного угла
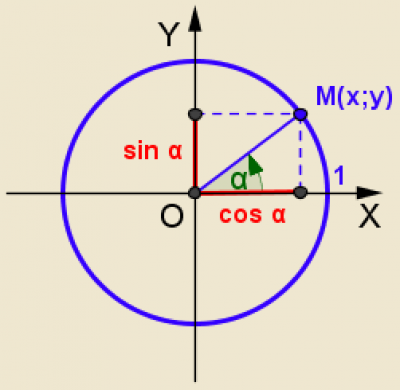
Тригонометрические функции произвольного угла
Рассмотрим окружность радиуса R с центром в начале прямоугольной системы координат Oxy.
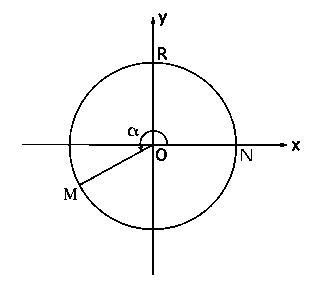
Положительным считают угол NOM, сторона OM которого получена из положительной полуоси Ox в результате поворота, осуществляемого в направлении движения против часовой стрелки.
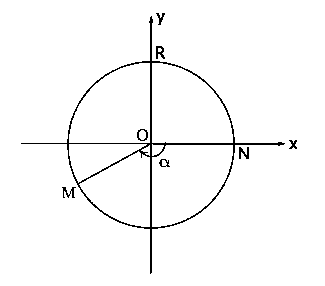
Отрицательным считают угол NOM, сторона OM которого получена из положительной полуоси Ox в результате поворота, осуществляемого в направлении, совпадающем с направлением движения часовой стрелки.
Если для координат точки М0, лежащей на окружности радиуса R с центром в начале координат O, ввести обозначение М0=(x0;y0), то по теореме Пифагора:
\(x_0^2 + y_0^2 = {R^2}.\)
Тогда можно сформулировать общее определение тригонометрических функций произвольного угла.
Синусом, косинусом, тангенсом и котангенсом произвольного угла α называют числа, определяемые по формулам:
\(\begin{gathered} \sin \alpha = \frac{{{y_0}}}{R}, \\ \cos \alpha = \frac{{{x_0}}}{R}, \\ tg\alpha = \frac{{{y_0}}}{{{x_0}}}, \\ ctg\alpha = \frac{{{x_0}}}{{{y_0}}}. \\ \end{gathered} \)
Замечание. Отметим следующее важное свойство тригонометрических функций синуса и косинуса произвольного угла:
\(\begin{gathered} - 1 \leqslant \sin \alpha \leqslant 1, \\ - 1 \leqslant \cos \alpha \leqslant 1. \\ \end{gathered} \)
Другие материалы по данной теме
Видео
Синус, косинус, тангенс и котангенс