Линейным неравенством с одной переменной называют выражение вида \(ax+b<cx+d.\) С помощью свойств неравенств его приводят к виду:

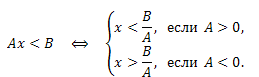
Если \(A=0,B>0,\) то неравенство имеет бесконечное множество решений.

Если же \(A=0,B<0,\) то неравенство не имеет решений.

Пример 1. Решить совокупность неравенств:

\(2(x-1)+3(2x+4)<4(x+7)+6.\)

Решение. Используя свойства неравенств, преобразуем данное неравенство и получим:

\(8x+10<4x+34\iff 4x<24 \iff x<6.\)

Ответ: \(x \in (-\infty;6).\)

Говорят, что несколько неравенств образуют систему неравенств, если следует найти все числа, каждое из которых является решением каждого из указанных неравенств.
Система:

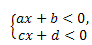
является примером системы двух линейных неравенств с одной переменной.

Пример 2. Решить систему неравенств:

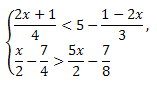
Решение.

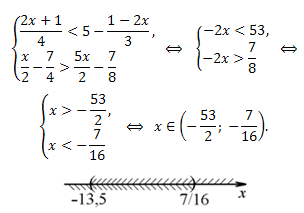
Ответ: \(x \in (-\frac{53}{2};-\frac{7}{16}).\)

Говорят, что несколько неравенств образуют совокупность неравенств, если следует найти все числа, каждое из которых является решением хотя бы одного из заданных неравенств.
 Совокупность неравенств:

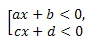
является примером совокупности двух линейных неравенств с одной переменной.

Пример 3. Решить систему неравенств:

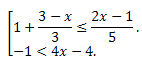
Решение.

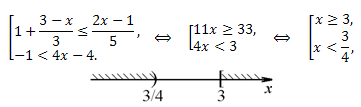
Ответ: \(x \in (-\infty;\frac{3}{4})\cup [3;+\infty).\)