Прежде чем перейти к решению неравенств, напомним основные определения и свойства числовых неравенств.
 Говорят, что число aбольше числа b, если разность a – b есть положительное число.
 Число aменьше числа b, если разность a – b отрицательна. Числовые неравенства обладают следующими свойствами:

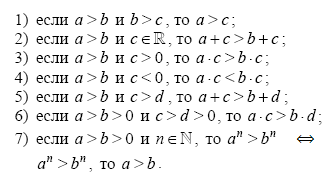
(В пункте 7) в случае нечётного числа n условие b > 0 избыточно.)
 Неравенством с одной переменной называют каждое из следующих выражений:

\(f(x)<g(x), (f(x)\leq g(x));\)

\(f(x)>g(x), (f(x)\geq g(x)).\)

Областью допустимых значений переменнойx называют общую часть областей определения функций f(x) и g(x).

Решением неравенства с одной переменной называют значение переменной, которое обращает его в верное числовое неравенство. Решить неравенство – значит найти все его решения или доказать, что их нет.
 Два неравенства называются равносильными, если множества их решений совпадают. (Неравенства, не имеющие решений, также равносильны.)

Например, неравенства \(f(x)<g(x), \)\(g(x)>f(x)\) равносильны, что записывается следующим образом:

== Неравенства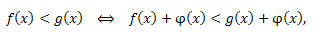

если области определения функций \(f(x),g(x),\phi(x)\) совпадают.

== Неравенства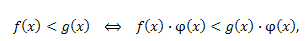 

если \(\phi(x)>0\) в области определения функций \(f(x),g(x).\)

== Неравенства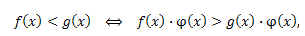 

если \(\phi(x)<0\) в области определения функций \(f(x),g(x).\)