В проводниках имеются электрически заряженные частицы – носители заряда (электроны в металлах, ионы в электролитах), способные перемещаться по всему объему проводника под действием внешнего электростатического поля. В настоящем разделе мы ограничимся рассмотрением твердых металлических проводников.

Носителями заряда в металлах являются электроны проводимости. Они возникают при конденсации паров металла за счет обобществления валентных электронов.

При отсутствии электростатического поля металлический проводник является электрически нейтральным – электростатическое поле, создаваемое положительными и отрицательными зарядами внутри него, компенсируется.

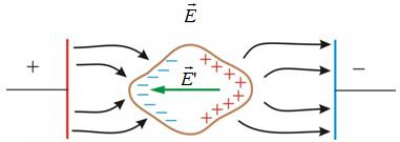
При внесении металлического проводника во внешнее электростатическое поле электроны проводимости перемещаются (перераспределяются) до тех пор, пока всюду внутри проводника поле электронов проводимости и положительных ионов не скомпенсирует внешнее поле.

Итак, в любой точке внутри проводника, находящегося в электростатическом поле, \(\vec E = 0\);\({\rm{d}}\varphi = 0\), т.е. \(\varphi = {\rm{const}}\), в идеальном проводнике диэлектрическая проницаемость Ɛ_МЕ →∞

На поверхности проводника напряженность \(\vec E\) (рис.) должна быть направлена по нормали к этой поверхности, иначе под действием составляющей E_τ, касательной к поверхности, заряды перемещались бы по проводнику, а это противоречило бы их статическому распределению.

Вне заряженного проводника поле есть, следовательно, должен быть вектор \(\vec E\), и направлен он перпендикулярно поверхности.

Итак, в установившимся состоянии в проводнике, помещенном
в электростатическое поле, имеем:

• Появление у заряженной поверхности на металле заряда противоположного знака – электростатическая индукция. Этот процесс очень краток ( ~ 10^–8 с).
• Электростатическое экранирование – внутрь проводника поле не проникает.
• Во всех точках внутри проводника Е = 0, а во всех точках на поверхности проводника \(E = {E_n}\,\,\,\,({E_\tau } = 0);\)
• Весь объем проводника, находящегося в электростатическом поле, эквипотенциален.

Действительно, в любой точке внутри проводника \(\frac{{{\rm{d\varphi }}}}{{{\rm{d}}l}} = - {\rm{E}} = 0\), следовательно, \(\varphi = {\rm{const}}\)

Поверхность проводника тоже эквипотенциальна: \({\phi _{\Pi {\rm O}{\rm B}}} = {\rm{const}}\), т.к. \(\frac{{{\rm{d}}\phi }}{{{\rm{d}}l}} = - {E_\tau } = 0\).

• Потенциал на поверхности проводника равен потенциалу внутри проводника.
• В заряженном проводникенекомпенсированныезаряды располагаются только на поверхности (их расталкивают кулоновские силы).

Можно доказать последнее утверждение формально: проведем внутри проводника произвольную замкнутую поверхность S, ограничив некоторый объем внутри проводника. Тогда, согласно теореме Остроградского – Гаусса, т.к. E = 0, суммарный заряд q этого объема равен 0:

\(q = \oint\limits_s {D{\rm{d}}S} = \oint\limits_s {E{\rm{\varepsilon }}{{\rm{\varepsilon }}_{\rm{0}}}{\rm{d}}S = 0} \).