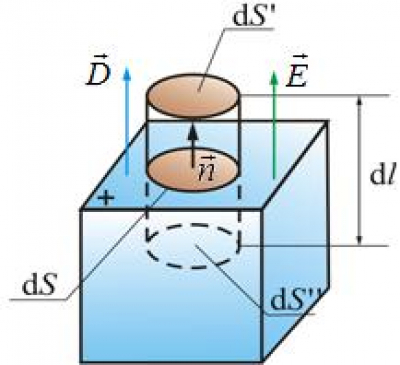
Выделим на поверхности S проводника площадку dS и построим на ней цилиндр с образующими, перпендикулярными к площадке dS, высотой dl (рис.):

\({\rm{d}}S' = {\rm{d}}S'' = {\rm{d}}S.\)

На поверхности проводника вектор напряженности поля \(\vec E\) и вектор электрического смещения \(\vec D = \varepsilon {\varepsilon _0}\vec E\) перпендикулярны поверхности. Поэтому поток \(\vec D\) сквозь боковую поверхность равен нулю.

Поток вектора электрического смещения \({\Phi _D}\) через \({\rm{d}}S''\) 

тоже равен нулю, т.к. \({\rm{d}}S''\) лежит внутри проводника, где \(\vec E = 0\) и, следовательно, \(\vec D = 0\). Отсюда следует, что поток \({\rm{d}}{\Phi _D}\) сквозь замкнутую поверхность равен потоку \(\vec D\) через \({\rm{d}}S'\):

\({\rm{d}}{\Phi _D} = {D_n}{\rm{d}}S.\)

С другой стороны, по теореме Остроградского – Гаусса

\({\rm{d}}{\Phi _D} = {\rm{d}}q = \sigma {\rm{d}}S,\)

где σ – поверхностная плотность зарядов на dS. Из равенства правых частей следует, что \({D_n} = \sigma \), тогда

\({E_n} = \frac{{{D_n}}}{{{{\rm{\varepsilon }}_{\rm{0}}}{\rm{\varepsilon }}}} = \frac{\sigma }{{{{\rm{\varepsilon }}_{\rm{0}}}{\rm{\varepsilon }}}}\)

Итак, напряженность поля вблизи поверхности заряженного проводника прямо пропорциональна поверхностной плотности зарядов.

Были рассмотрены поля, создаваемые плоскостью, цилиндром, шаром, и везде получили, что E ~ σ. Этот вывод является общим, т.к. произвольные поверхности есть комбинации указанных выше простейших поверхностей.