Потенциальная энергия – это механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. Если на тело (материальную точку) в каждой точке пространства действует определенная сила, то всю совокупность сил называют силовым полем. Если силы не зависят от времени, силовое поле называется стационарным. Например, тело массой m, расположенное вблизи поверхности Земли, испытывает действие силы тяжести \(m\vec g\). Величину и направление силы тяжести можно считать приблизительно одинаковыми во всех точках пространства вблизи поверхности Земли. Тело находится в однородном поле силы тяжести. 

Пусть взаимодействие между телами осуществляется с помощью силовых полей (например, поле гравитационных сил, поле упругих сил), которые обладают следующим свойством: работа, совершаемая силами при перемещении тела из одного положения в другое, не зависит от траектории тела, а зависит только от начального и конечного положения тела. Такие силы называются консервативными. Поле консервативных сил называется консервативным.

Если работа, совершаемая силой, зависит от траектории тела, то такая сила называется неконсервативной; ее примером является сила трения.

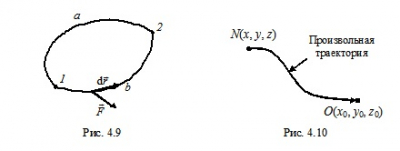
Покажем, что при перемещении тела в консервативном поле работа консервативных сил по замкнутой траектории равна нулю (рис. 4.9).

Работа консервативной силы не зависит ни от вида траектории точки между ее начальным 1 и конечным 2 положениями, ни от закона движения материальной точки по траектории: \({A_{1 - a - 2}} = {A_{1 - b - 2}} = {A_{1 - 2}}\), где \({A_{1 - a - 2}}\) и \({A_{1 - b - 2}}\) – работа консервативной сила при перемещении материальной точки из 1 в 2 по траекториям 1–а–2 и 1–b–2. Изменение направления движения материальной точки на противоположное вызывает изменение знака проекции консервативной силы \(\vec F\) на направление перемещения, поэтому знак элементарной работы также изменяется: \(\delta A = (\vec F{\rm{d}}\vec r)\). Следовательно, \({A_{1 - b - 2}} = - {A_{2 - b - 1}}\), поэтому работа консервативной силы вдоль замкнутой траектории 1–b–2–a–1 равна нулю:

\({A_{1 - b - 2 - a - 1}} = {A_{1 - b - 2}} + {A_{2 - a - 1}} = - {A_{2 - b - 1}} + {A_{2 - a - 1}} = 0\).

Точки 1 и 2, а также участки замкнутой траектории 1–a–2 и 2–b–1 можно выбирать совершенно произвольно. Таким образом, работа консервативной силы на произвольной замкнутой траектории L точки ее приложения равна нулю:

\(\oint\limits_L {(\vec F{\rm{d}}\vec r) = 0} \). (4.22)

 В этой формуле кружок на знаке интеграла показывает, что интегрирование производится по замкнутому контуру L.

Пусть имеется консервативное силовое поле. Материальная точка (тело) расположена в точке N(x, y, z) этого поля (рис. 4.10). Выберем произвольную точку О этого поля (ее координаты x₀, y₀, z₀) и назовем ее началом отсчета потенциальной энергии. В точке О потенциальная энергия материальной точки равна нулю.

Потенциальной энергией материальной точки в точке Nконсервативного поля называется работа сил поля, совершаемая при перемещении материальной точки из точки N в точку О, принятую за начало отсчета потенциальной энергии:\({E_\Pi } = \int\limits_N^O {(\vec F{\rm{d}}\vec r)} \), где \(\vec F\) – сила поля; интеграл вычисляется по произвольной траектории между точками N и О.

Так как поле консервативное, то потенциальная энергия является только функцией координат x, y, z точки поля, в которой расположена материальная точка.

Если материальная точка под действием консервативных сил поля перемещается из произвольного начального положения 1 в произвольное конечное положение 2 (рис. 4.11), то работа этих сил равна убыли потенциальной энергии материальной точки: \({{\rm A}_{1 - 2}} = {{\rm E}_{\Pi 1}} - {{\rm E}_{\Pi 2}}\), где Е_П1 и Е_П2 – потенциальная энергия материальной точки в начальном и конечном положениях. Так как работа консервативных сил не зависит от формы траектории, то найдем работу консервативных сил по двум траекториям, одна из которых проходит через точку О – начало отсчета потенциальной энергии. Обозначим \({A_{1 - 2}}\) – работу по траектории 1–2, \({A_{1 - O - 2}}\) – работу по траектории 1–О–2. Так как поле консервативное, то \({A_{1 - 2}} = {A_{1 - O - 2}}\).

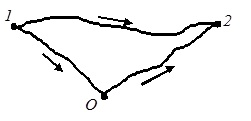
Рис. 4.11.

Представим \({A_{1 - O - 2}}\) как сумму работ на участках 1–О и О–2 по траектории 1–О–2, получим \({A_{1 - 2}} = {A_{1 - O - 2}} = {A_{1 - O}} + {A_{O - 2}} = {A_{1 - O}} - {A_{2 - O}}\).

Из определения потенциальной энергии \({A_{1 - O}} = {E_{\Pi 1}},\quad {A_{2 - O}} = {E_{\Pi 2}}\), тогда

\({A_{1 - 2}} = {E_{\Pi 1}} - {E_{\Pi 2}} = - ({E_{\Pi 2}} - {E_{\Pi 1}}) = - \Delta {E_\Pi }\). (4.23)

Элементарная работа консервативных сил

\(\delta A = - {\rm{d}}{E_\Pi }\). (4.24)

Выражения (4.23) и (4.24) определяют связь работы консервативных сил с изменением потенциальной энергии поля (в интегральной и дифференциальной формах соответственно).

Итак, работа консервативной силы определяется разностью потенциальной энергии тела в начальной и конечной точках пути. При элементарном перемещении работа равна минус изменению потенциальной энергии:

\({\rm{d}}A = \left( {\vec F{\rm{d}}\vec r} \right) = - {\rm{d}}{E_\Pi }\). (4.25)

Знак минус говорит о том, что работа совершается за счет убыли потенциальной энергии.

Работа консервативных сил на конечном участке пути 1–2

\({A_{12}} = \int\limits_1^2 {\left( {\vec F{\rm{d}}\vec r} \right) = - \left( {{E_{\Pi 2}} - {E_{\Pi 1}}} \right)} = {E_{\Pi {\rm{1}}}} - {E_{\Pi {\rm{2}}}}\). (4.26)

Потенциальная энергия – функция, которая определяется с точностью некоторой произвольной постоянной, определяющей нулевой уровень потенциальной энергии. Так как в формулу работы консервативной силы входит только разность значений Е_П в двух положениях частицы, то нулевой уровень отсчета энергии выбирают произвольно. То есть потенциальную энергию тела в каком-то определенном положении считают равной нулю. Энергию тела в других положениях отсчитывают относительно нулевого уровня. Тело, находящееся в поле консервативных сил, обладает потенциальной энергией E_п относительно нулевого уровня потенциальной энергии.

Конкретный вид функции E_п зависит от характера силового поля.

Для определения потенциальной энергии тела (материальной точки) в консервативном силовом поле необходимо выбрать положение начала отсчета нулевого уровня потенциальной энергии и вычислить работу силы при перемещении по произвольной траектории в этом поле из данной точки поля в точку отсчета нулевого уровня потенциальной энергии.