Потенциальная энергия тела массой m, поднятого на высоту h над поверхностью Земли.

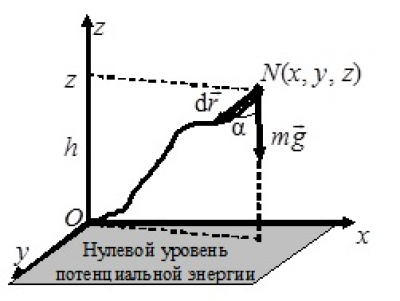
Пусть материальная точка (тело) массой m находится в точке N(x, y, z) однородного поля силы тяжести (рис.). В качестве начала отсчета потенциальной энергии выберем точку О начала декартовой системы координат. Плоскость xOy совместим с поверхностью Земли.

Потенциальная энергия материальной точки (тела) в точке N поля равна работе силы тяжести, совершаемой при перемещении тела из точки N с координатами x, y, z в точку O с координатами x₀ = y₀ = z₀ = 0. Тогда элементарная работа равна

\(\delta A = \left( {m\vec g{\rm{d}}\vec r} \right) = mg\left| {{\rm{d}}\vec r} \right| \cdot \cos \alpha = - mg{\rm{d}}z\),

где \( - {\rm{d}}z = \left| {{\rm{d}}\vec r} \right| \cdot \cos \alpha \)

При перемещении тела из точки N в точку О работа силы тяжести равна

\(A = - \int\limits_z^0 {mg{\rm{d}}z} = - mg(0 - z) = mgz = mgh\)

Работа силы тяжести при падении тела на Землю равна потенциальной энергии 

\({E_\Pi } = mgh\)

если за нуль принята потенциальная энергия тела, лежащего на Земле.