Дробно-рациональным неравенством называется неравенство вида:

\(\frac{f(x)}{\phi(x)}>K,\)

где \(f(x),\phi (x)\) - многочлены степени n и m; K – число.

Для решения данных неравенств удобно использовать следующую схему:

• Указать область допустимых значений переменной x, \(\phi(x)\neq 0.\) Пусть это будет \(x\in(a,b).\)
• 
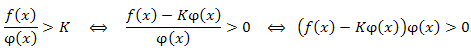
• Разложить левую часть неравенства (если это возможно) на множители \((x-x_1)^{k_1}(x-x_2)^{k_2}...(x-x_r)^{k_r}t(x)>0,\)

где t(x) – многочлен, не имеющий действительных корней в области определения неравенства.

• Использовать метод интервалов:

1. на координатной прямой отметить область определения неравенства \(x\in(a,b).\) и разбить ее точками, соответствующими нулям функции \((f(x)-K\phi(x))\phi(x)\) на интервалы, в каждом из которых эта функция сохраняет знак;
2. определить знак функции, например, в крайнем справа интервале \((x_r,b)\);
3. переходя от интервала \((x_r,b)\) к интервалу \((x_{r-1},x_r)\), изменить знак функции в интервале \((x_{r-1},x_r)\), если множитель входит в разложение в нечетной степени, и не менять знак, если множитель входит в разложение в четной степени. Аналогично определить знак функции в интервале \((x_{r-2},x_{r-1})\) и т. д.

Метод интервалов можно использовать также для решения квадратных неравенств.