Пример 1. Решить неравенство:

\((2x^2+3x+4)(x+3)\geq0.\)

Решение. Решаем уравнение:

\((2x^2+3x+4)(x+3)=0.\)

Дискриминант уравнения \((2x^2+3x+4)=0\) равен D=-23, следовательно, \((2x^2+3x+4)>0\) при любых \(x \in(-\infty;x_1)\cup (x_2;+\infty).\) И исходное неравенство выполняется при x + 3 ≥0, т. е. при x ≥ –3.
Ответ: \(x \in[-3;+\infty).\)

Пример 2. Решить неравенство:

\((25x-x^3)(4-x^2)\leq0.\)

Решение. Разложим левую часть неравенства на множители:

\(x(5-x)(5+x)(2-x)(2+x)\leq0.\)

Найдём корни многочлена:

\(x=0,x=5,x=-5,x=-2.\)

Определим знаки многочлена на каждом интервале:

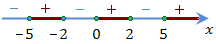
Ответ: \(x \in(-\infty;-5]\cup [-2;0]\cup [2;5].\)

Пример 3. Решить неравенство:

\((x^2-4x+4)(3x^2-2x-1)\leq0.\)

Решение. Решаем уравнение:

\(3x^2-2x=0:x=1,x=-1/3,\)

разложим левую часть неравенства на множители:

\((x-2)^2(x-1)(x+1/3)\leq0.\)

Определим знаки многочлена на каждом интервале:

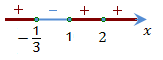
Ответ: \(x \in [-1/3;1]\cup \{2\}.\)

Пример 4. Решить неравенство:

\(\frac{21}{x+1}<\frac{16}{x-2}-\frac{6}{x}.\)

Решение. Находим ОДЗ:

\(x\neq-1,x\neq-2,x\neq0.\)

Перенесём всё в левую часть и приведём к общему знаменателю. Получим неравенство:

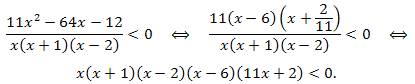
Определим знаки многочлена на каждом интервале:

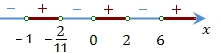
Ответ: \(x \in(-\infty;-1)\cup (-2/11;0)\cup (2;6).\)

Пример 5. Решить неравенство:

\(\frac{x^2(x-1)(x+3)^3(x-4)^4}{x^2+1}\geq0.\)

Решение. Находим ОДЗ: \(x \in R.\)

Поскольку \(x ^2+1>0\) при любом х, то исходное неравенство равносильно неравенству:

\(x^2(x-1)(x+3)^3(x-4)^4\geq0.\)

Найдём нули многочлена:

\(x = 0,x=-3,x=4.\)

Определим знаки многочлена в полученных интервалах:

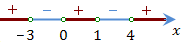
Ответ: \(x \in(-\infty;-3)\cup (1;4)\cup (4;+\infty).\)