Иррациональным уравнением называется уравнение, содержащее неизвестную под знаком радикала.
 Для решения иррациональных уравнений могут быть использованы следующие методы: метод возведения радикала в степень, метод замены переменной, метод приведения к смешанной системе, содержащей уравнения и неравенства. Приведём схемы и приемы решения некоторых видов уравнений.

1. Иррациональное уравнение вида \(\sqrt[2n]{f(x)}=g(x)\) равносильно системе:

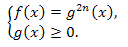
2. Уравнение вида \(\sqrt[2n]{f(x)}=\sqrt[2n]{g(x)}\) равносильно системе:

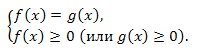
Пример 1. Решить уравнение:

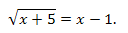
Решение. В соответствии со схемой первого пункта имеем:

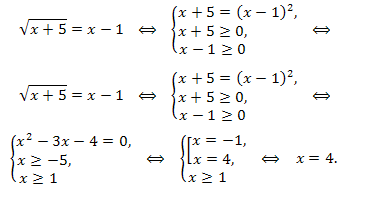
Ответ: x = 4.

Пример 2. Решить уравнение:

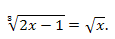
Решение.

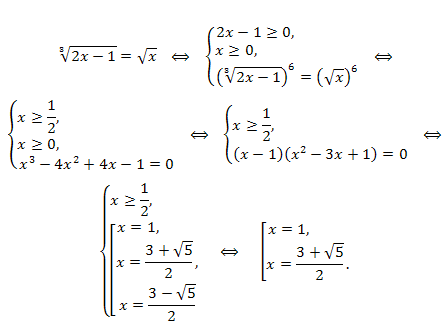
Ответ: \(x=1;x=\frac{3+\sqrt{5}}{2}.\)

Пример 3. Решить уравнение:

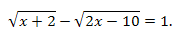
Решение. Находим область допустимых значений переменной х:

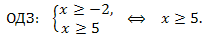
Преобразуем уравнение так, чтобы обе его части стали неотрицательными:

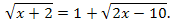
Тогда после возведения обеих частей уравнения в квадрат получим уравнение, равносильное данному на ОДЗ:

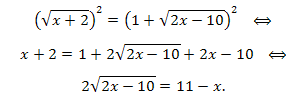
К полученному уравнению применяем первую схему:

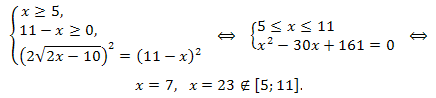
Ответ: x = 7.

Замечание. В некоторых случаях отыскание ОДЗ является процессом не менее трудоемким, чем решение уравнения. Тогда можно решить уравнение и ограничиться проверкой его корней, что особенно важно в случае возведения обеих частей уравнения в четную степень.