Пример. Решить уравнение:

\(x^2+3x-10+3\sqrt{x(x+3)}=0.\)

Решение. Заметив, что \(x(x+3)=x^2+3x\), сделаем замену переменной \(\sqrt{x^2+3x}=t;t\geq0;\) и решим уравнение:

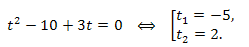
Переходим к переменной x:

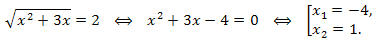
Так как \(t=-5<0,\) то \(\sqrt{x^2+3x}\neq-5.\)

Ответ: x = –4; x = 1.

При решении иррациональных уравнений для упрощения решения можно использовать следующие свойства функций, входящих в уравнение.
Если функция \(\phi(x)\) строго возрастает на промежутке X и \(\phi(x_0)\in X\) для любого \(x_0\in X\), то уравнения \(\phi(x)=x\) и \(\phi(\phi(x))=x\) равносильны на промежутке X.

Пример. Решить уравнение:

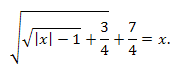
Решение. \(x\in [\frac{7}{4};+\infty),\) получаем:

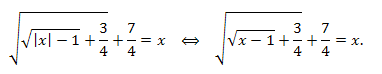
Представив левую часть уравнения в виде:

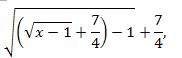
убеждаемся, что она является композицией \(\phi(\phi(x))\), где \(\phi(x)=\sqrt{x-1}+\frac{7}{4}.\)

Проверяем условия, которым должна удовлетворять функция \(\phi(x)\). Очевидно, что \(\phi(x)=\sqrt{x-1}+\frac{7}{4}.\) – строго возрастающая на области её определения x ≥ 1.

Убедимся, что для любого \(x\in [\frac{7}{4};+\infty),\) значение функции \(\phi(x)\) принадлежит множеству \( [\frac{7}{4};+\infty)\) В самом деле, для любого значения \(x\geq \frac{7}{4}\) значение \(\phi(x)=\sqrt{x-1}+\frac{7}{4} \geq \frac{7}{4}.\) Следовательно, функция \(\phi(x)\) отображает множество \([\frac{7}{4};+\infty)\) в себя. Поэтому с учетом равносильности уравнений \(\phi(x)=x\) и \(\phi(\phi(x))=x\) имеем:

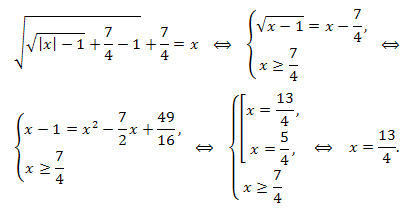
Ответ: \(x=\frac{13}{4}.\)

Пример 6. Решить уравнение:

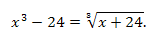
Решение. ОДЗ: \(x\in R\). Выполним равносильное преобразование уравнения:

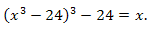
амечаем, что левая часть уравнения представляет собой композицию \(\phi(\phi(x))\) функции \(\phi(x)=x^3-24\), которая является строго возрастающей на R. Кроме того, для всех \(x\in R;\phi(x) \in R\), т. е. функция \(\phi(x)\) отображает множество R в себя. Поэтому:

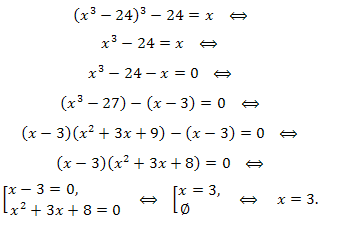
Ответ: \(x=3.\)