Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля.

Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов (опыт Толмена и Стьюарта).

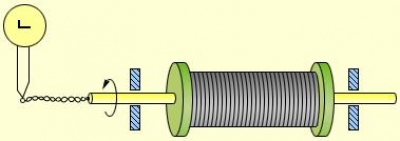
Катушка с большим числом витков тонкой проволоки (рис.) приводилась в быстрое вращение вокруг своей оси. Концы катушки с помощью гибких проводов были присоединены к чувствительному баллистическому гальванометру. Раскрученная катушка резко тормозилась, и в цепи возникал кратковременных ток, обусловленный инерцией носителей заряда. Полный заряд, протекающий по цепи, измерялся гальванометром.

При торможении вращающейся катушки на каждый носитель заряда e массой m действует тормозящая сила, которая играет роль сторонней силы, т.е. силы неэлектрического происхождения:

\(F = - m\frac{{{\rm{d}}\upsilon }}{{{\rm{d}}t}}\).

Сторонняя сила, отнесенная к единице заряда, по определению является напряженностью Е_СТ поля сторонних сил:

\({E_{CT}} = - \frac{m}{e}\frac{{{\rm{d}}\upsilon }}{{{\rm{d}}t}}\).

Следовательно, в цепи при торможении катушки возникает электродвижущая сила Е

\({\rm E} = {E_{CT}}l = - \frac{m}{e}\frac{{{\rm{d}}\upsilon }}{{{\rm{d}}t}}l\).

За время торможения катушки по цепи протечет заряд q, равный

\(q = \int {I{\rm{d}}} t = \frac{1}{R}\int {{\rm E}\,{\rm{d}}} t = \frac{m}{e}\frac{{l{{\rm{\upsilon }}_0}}}{R}\),

где l – длина проволоки катушки; I – мгновенное значение силы тока в катушке; R – полное сопротивление цепи; \({\upsilon _0}\) – начальная линейная скорость проволоки.

Хорошая электропроводность металлов объясняется высокой концентрацией свободных электронов, равной по порядку величины числу атомов в единице объема.

Предположение о том, что за электрический ток в металлах ответственны электроны, возникло значительно раньше опытов Толмена и Стюарта. Еще в 1900 г. немецкий ученый П. Друде на основе гипотезы о существовании свободных электронов в металлах создал электронную теорию проводимости металлов. Эта теория получила развитие в работах голландского физика Х. Лоренца и носит название классической электронной теории. Согласно этой теории электроны в металлах ведут себя, как электронный газ, во многом похожий на идеальный газ.

Электронный газ заполняет пространство между ионами, образующими кристаллическую решетку металла. Из-за взаимодействия с ионами электроны могут покинуть металл, лишь преодолев так называемый потенциальный барьер. Высота этого барьера называется работой выхода.

При обычных (комнатных) температурах у электронов не хватает энергии для преодоления потенциального барьера. Согласно теории Друде – Лоренца электроны обладают такой же средней энергией теплового движения, как и молекулы одноатомного идеального газа. Это позволяет оценить среднюю скорость теплового движения электронов по формулам молекулярно-кинетической теории: ʋ_теп = 10⁵ м/с.

При наложении внешнего электрического поля в металлическом проводнике, кроме теплового движения электронов, возникает их упорядоченное движение (дрейф), т.е. электрический ток. Величина дрейфовой скорости электронов лежит в пределах 0,6–6 мм/c. Таким образом, средняя скорость упорядоченного движения электронов в металлических проводниках на много порядков меньше средней скорости их теплового движения.

Малая скорость дрейфа не противоречит опытному факту, что ток во всей цепи постоянного тока устанавливается практически мгновенно. Замыкание цепи вызывает распространение электрического поля со скоростью c = 3*10⁸ м/с. Через время \(\tau = l/c\) (l – длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля, и в ней начинается упорядоченное движение электронов.

В классической электронной теории металлов предполагается, что движение электронов подчиняется законам механики Ньютона. В этой теории пренебрегают взаимодействием электронов между собой, а их взаимодействие с положительными ионами сводят только к соударениям. Предполагается также, что при каждом соударении электрон передает решетке всю накопленную в электрическом поле энергию, и поэтому после соударения он начинает движение с нулевой дрейфовой скоростью.

Несмотря на то, что все эти допущения являются весьма приближенными, классическая электронная теория качественно объясняет законы электрического тока в металлических проводниках – закон Ома, закон Джоуля – Ленца – и объясняет существование электрического сопротивления металлов.

Закон Ома:

\(I = enS{\vec \upsilon _D} = \frac{1}{2}\frac{{{e^2}\tau nS}}{m}E = \frac{{{e^2}\tau nS}}{{2ml}}U\).

Электрическое сопротивление проводника:

\(R = \frac{{2m}}{{{e^2}n\tau }}\frac{l}{S}\).

Закон Джоуля – Ленца:

\(\Delta Q = \frac{{nSl\Delta t}}{\tau }\frac{{{e^2}{\tau ^2}}}{{2m}}{E^2} = \frac{{n{e^2}\tau S}}{{2m}}{U^2}\Delta t = \frac{{{U^2}}}{R}\Delta t\).

Однако в ряде вопросов классическая электронная теория приводит к выводам, находящимся в противоречии с опытом. Эта теория не может, например, объяснить, почему молярная теплоемкость металлов, также как и молярная теплоемкость диэлектрических кристаллов, равна 3R (закон Дюлонга и Пти). Классическая электронная теория не может также объяснить температурную зависимость удельного сопротивления металлов: теория дает \(\rho {\rm{~}}\sqrt {\rm{T}} \), в то время как из эксперимента получается зависимость ρ ~ T.

Наиболее ярким примером расхождения теории и опытов является сверхпроводимость.