Для описания движения материальной точки надо знать, в каких местах пространства эта точка находилась и в какие моменты времени она проходила то или иное положение.

Определить положение тела можно только по отношению к другим телам. Если тело находится в пространстве, где нет других тел, то мы ничего не можем сказать о движении тела. В этом случае нет ничего, по отношению к чему тело могло бы изменить свое положение. Тело, по отношению к которому рассматривается движение других тел, называется телом отсчета. Тело отсчета – условно неподвижное тело, относительно которого определяется положение движущегося тела.

Совокупность тела отсчета и часов называется системой отсчета. С системой отсчета связывают систему координат. Наиболее часто используется декартова система координат, где x – ось абсцисс (абсцисса), y – ордината, z – аппликата (рис. 1.1). 

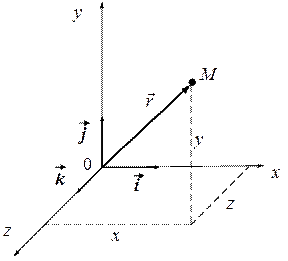
Положение материальной точки характеризуется тремя координатами (x, y, z) или радиусом-вектором \(\vec r = x\vec i + y\vec j + z\vec k\), где \(\vec i,\vec j,\vec k\)– единичные вектора (орты):

\(\left| {\vec i} \right| = \left| {\vec j} \right| = \left| {\vec k} \right| = 1\); \(r = \sqrt {{x^2} + {y^2} + {z^2}} .\)

При движении материальной точки ее координаты, а значит
и \(\vec r\) – вектор, изменяются со временем.

Движение материальной точки определяется скалярными уравнениями

\(x = x\left( t \right);\begin{array}{*{20}{c}}{}&{y = y\left( t \right);\begin{array}{*{20}{c}}{}&{z = z\left( t \right)}\end{array}}\end{array}\) (1.1)

или векторным уравнением

\(\vec r = \vec r\left( t \right).\) (1.2)

Уравнения (1.1) и (1.2) называются кинематическими уравнениями движения материальной точки.