Длина отрезка траектории АВ, пройденного материальной точкой, называется длиной пути\(\Delta S\). Надо помнить, что перемещение \(\Delta \vec r\) – вектор, а длина пути \(\Delta S\) – скаляр.

При прямолинейном движении модуль перемещения равен пройденному пути:

\(\left| {\Delta \vec r} \right| = \Delta S\). (1.3)

При криволинейном движении

\(\left| {\Delta \vec r} \right| < \Delta S\). (1.4)

Но если перемещение происходит в течение бесконечно малого промежутка времени, т.е. когда \(\Delta \vec r\) стремится к нулю, то в этом случае модуль бесконечно малого перемещения можно принять равным бесконечно малой длине пути для любого произвольного движения:

\(\left| {{\rm{d}}\vec r} \right| = {\rm{d}}S\). (1.5)

Если материальная точка участвует в нескольких перемещениях (рис. 1.3), то результирующее перемещение равно векторной сумме перемещений, совершаемых материальной точкой в каждом из движений в отдельности:

\(\Delta \vec r = \sum {\Delta {{\vec r}_i}} \); (1.6)

\(\Delta \vec r = \Delta {\vec r_1} + \Delta {\vec r_2}\). (1.7)

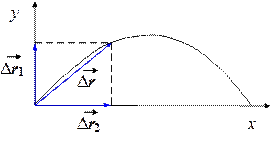
Рис. 1.3