Физика
2.1.2. Тепловое движение атомов и молекул вещества
Средняя длина свободного пробега молекул газа
|
|
|
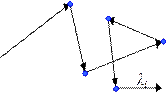
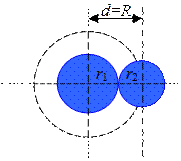
| Рис. 9.7 | Рис. 9.8 |
Если \({n_0}\) – концентрация молекул, то число молекул в объёме \(V\) равно \(4\pi {r^2}l{n_0}\), это число будет равно числу столкновений \(z\), т.к. движущаяся молекула столкнётся со всеми молекулами, центры которых заключены в ломаном цилиндре. Итак, \(z = 4\pi {r^2}l{n_0}\). Если учесть, что все молекулы движутся одновременно, то расчёты дают формулу
\(z = 4\sqrt 2 \pi {r^2}l{n_0} = \sqrt 2 \pi {\sigma ^2}l\,{n_0}\). (9.40)
Тогда
\(\bar \lambda = \frac{1}{{4\sqrt 2 \pi {r^2}{n_0}}}\) или \({\rm{\bar \lambda }} = \frac{1}{{\sqrt 2 \pi {\sigma ^2}{n_0}}}\). (9.41)
Из формулы видно, что длина свободного пробега молекул обратно пропорциональна концентрации молекул: 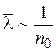 ; т.к. давление \(P = {n_0}kT\), то, следовательно,
; т.к. давление \(P = {n_0}kT\), то, следовательно, 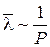 .
.
Если уменьшать давление \(P\), то средняя длина свободного пробега \(\bar \lambda \) увеличивается.
Можно откачать газ из сосуда так, что линейные размеры сосуда \(L < {\rm{\bar \lambda }}\). Тогда молекулы будут летать от стенки к стенке, не испытывая столкновений. В этом случае говорят, что в сосуде вакуум.
Другие материалы по данной теме
Формула
\(\Delta n = \frac{4}{{\sqrt \pi }}n{e^{ - \frac{{{v^2}}}{{v_{в\rm{}}^2}}}}\frac{{{v^2}}}{{v_{в\rm{}}^3}}\Delta v\)