Название физической величины: амплитуда гармонически изменяющейся физической величины; амплитудное значение гармонического колебания; максимальное по модулю значение физической величины, изменяющейся по гармоническому закону.

Обозначение физической величины: А – школьное обозначение. Другие обозначения – х₀, или обозначение любой другой физической величины, изменяющейся по гармоническому закону. Например, если по гармоническому закону изменяется сила электрического тока, то уравнение записывается так: I(t)=I₀sin(ωt+φ₀).

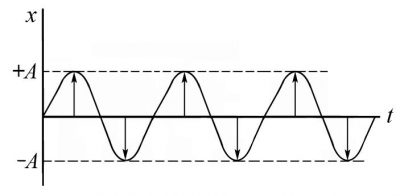
Формула связи физических величин: амплитуда – это максимальное значение физической величины, изменяющейся по гармоническому закону. Для гармонического колебания, описанного с помощью функции синуса, физическая величина х принимает амплитудные по модулю значения в следующих случаях:

х (t)= х ₀sin(ωt+φ₀). х(t₀)= х₀, или х(t_n+nT/2)=А в те моменты времени t_n, когда sin(ωt_n+φ₀)=±1. t_n=\(\frac{{\frac{\pi }{2} + \pi n - {\phi _0}}}{\omega }\), где n=0,1,2,3…

Расшифровка формулы или способ измерения: в те моменты времени, когда фаза (ωt_n+φ₀) принимает значения, равные +πn, где n=0,1,2,3…, а именно

(ωt_n+φ₀)= \(\frac{\pi }{2}\)+πn (1)

и синус, соответственно, принимает значения, равные sin(ωt_n+φ₀)=+ 1. Докажем это. Выразим из (1) те значения времени, когда синус по модулю принимает максимальные значения:

t_n=\(\frac{{\frac{\pi }{2} + \pi n - {\phi _0}}}{\omega }\), где n=1,2,3…

Теорема доказана.

Вектор или скаляр физическая величина: скаляр положительный, когда n – четное число n=2k , где k =0,1,2,3… И отрицательный, когда n – нечетное число n=2k+1, где k =0,1,2,3…

Размерность физической величины: размерность совпадает с размерностью той физической величины, которая испытывает гармонические колебания.